

Books (1991-2003):
from Mathematical Chemistry
Series
(click to view TOC)







More books...
What is Mathematical Chemistry?
Read about the yet unclear definition of the term (Croatica Chemica Acta, pdf)
Some useful links about mathematical chemistry (DMOZ project).
One more collection of links (Geometry.net)
Report (1995): Mathematical Challenges from Theoretical/Computational Chemistry.
Mathematical Chemistry meetings:
- International Meetings on Mathematical Chemistry (cancelled in 1999):
Athens (1987), Galveston (1989), Bled (1991), Kansas City (1993), Pitlocry (1995), Girona (1997)- DIMACS Workshop
(New Brunswick, 1998)- Math/Chem/Comp meetings: Dubrovnik
(1986-2005)- Indo-US Workshops on Mathematical Chemistry
(1998, 2000, 2003, 2005)
Who is who in Mathematical Chemistry
(Selected and very subjective alphabetic listing of some individuals and groups involved in the various topics of mathematical chemistry, mainly in chemical graph theory. With some bio-/biblio-/graphic links.) In progress.
Links to mathematical chemistry papers published by Eugene Babaev
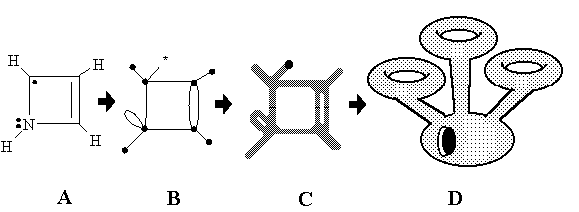
Intuitive Chemical Topology Concepts
Consider a molecular "ball-and-stick" model made from rubber tubes. What happens if we "inflat" such a model?We shall get a surface (a manifold) with intriguing properties. One particular feature of this approach is that the Euler characteristic of such a manifold will be preserved in chemical reactions...
Abstracts:
In the present paper we treat chemical similarity in terms of the homeomorphism concept and electron count rules. We suggest a novel interrelationship between molecular graphs and molecular 2D surfaces by direct mapping of chemical structures (like the Lewis dot formulas) to the specific 2D manifolds and pseudomanifolds. We define this mapping in such a way that the lone pairs, free radical centers, and multiple and multicentered bonds serve as the intrinsic topological invariants of the 2D models. This approach allows us to apply the homeomorphism concept to chemical problems in a new way, classifying molecular structures and reactions from the viewpoint of the topology of surfaces.
The structure of the paper is the following. Section 2 recalls several concepts of the graph theory and topology of surfaces, necessary for further discussion, and Section 3 is the overview of the common types of molecular graphs and molecular surfaces used in chemistry. In Section 4 we treat the concepts of free radicals, lone pairs, and multiple bonds as intuitively topological concepts, whereas Section 5 provides an explicit definition and visualization of their topology on the graph-theoretical level. In Section 6 we suggest an explicit mathematical concept of molecular topoid, which visualizes the lone pairs, free radicals, and multiple bonds as sorts of “holes” in an appropriate 2D surface. The topoid (a “rubber 2D molecule” without geometry) is a novel combinatorial 2D image of molecule, intermediate between ordinary surfaces and graphs. Operations on topoids (resembling cut-and-paste operations of a topologist with imaginary 2D manifolds) reflect the key types of formation and cleavage of chemical bonds. In Section 7 we suggest a novel conservation law, the invariance of Euler characteristic of molecular topoids, and use it for classifying the chemical reactions. Section 8 has the goal to illustrate, how the homeomorphism of topoids brings together diverse molecular similarity types in a unique manner. In Section 9 we prove that the explicit 2D image of a graph should be a surface with embedded Jordan curves, and in Section 10 the nonequivalent types of embedding are used to expand the common principles of 2D modeling in chemistry. In Section 11 we use the generalized concept of hypertopoids to classify the structure and reactivity of molecules with multicentered and delocalized bonds on the 2D level. Finally, in Section 12 we investigate the possibility of 2D modeling of the excited states of molecules with several unpaired electrons by using nonorientable surfaces.Table of Contents. Full text
The Alternation Rule: An Old Heuristic Principle or the New Conservation Law?
How many conservation laws exist in chemistry? Not so much: conservation of mass, charge, energy, orbital symmetry... Above we discussed the conservation of the Euler characteristics. Anything else? Let us examine one more: conservation of "chemical parity"
Consider a set of objects closed in relation to an operation of their change. A group, an algebra? No. The objects are some specific molecules with bipartite graphs (which follow so-called "alternation rule", and the operation is a polar chemical reaction.

From Introduction:
We will attempt in this paper to find an example of a closed set where it was earlier not looked for or was not noted. We will show that among structures, habitual to the glance of organic chemists, a class of molecules can be mathematically rigidly separated, possessing certain "rhythmic" similarity of electronic structure, associated with alternation of polar (donor and acceptor) centers. As an example of the operation of changes of such objects (called superconsonant below), we will examine general polar reactions, including stages of heterolytic formation and/or cleavage of bonds. The main idea of this approach is that the indicated set with certain assumptions can in fact be considered "almost closed" in relation to the indicated operation of changes. In its turn, such an assertion is equivalent to a new principle, nontrivial for organic chemistry, of retention of the topological property of polar bipartition (charge alternation) in polar processes. The formulation of the model is preceded by a review of early papers, devoted to the principle of alternation and the problem of consonance, in no way finding reflection to date in the domestic literature.
Abstracts:
Early concepts and models of polarity alternation along the chains with polar groups are critically reviewed. The proposed new model describes alternation along the chains as the result of specific mutual disposition of Lewis' basic and acidic centres. Identical results can be obtained from both the models of polar bipartite multigraphs and the model of "ions in molecule". This gives rise to separate the specific class of molecules and ions (called "super-consonant"), whose polar bipartite structure strictly determine possibility of their presentation as ion assemblage. The author's quantum chemical AM1 calculations proved charge alternation even at the structures of non-polar consonant molecules and/or their ions. The hypothesis of "alternation conservation" in ionic processes is claimed, that permits one to consider the consonant set of molecules to be closed (for the p-elements of 2-row) in relation to polar reactions. Wide applications of this hypothesis and rare counterexamples are discussed. Simple genetical interrelationship among the structures of the super consonant series is proposed as the model of computer generation of non-trivial synthetic equivalence types.
Concept of Chemical Periodicity: from Mendeleev Table to Molecular Hyper-Periodicity Patterns (with R. Hefferlin)
Can we built a Periodic Table of Molecules? How may it look like? Is it multidimensional?
Trying to answer these questions we should recall that classical language of chemistry is more deeply related to mathematics than it is commonly considered. Indeed, a chemical formula is nothing else but a partition of a natural number, and the Lewis dot diagram from mathematical viewpoint is only a sort of a pseudograph. Let us order these mathematical objects (partitions or graphs) on the plane and analyse the chemical trends at this flat "hyperperiodic" table...
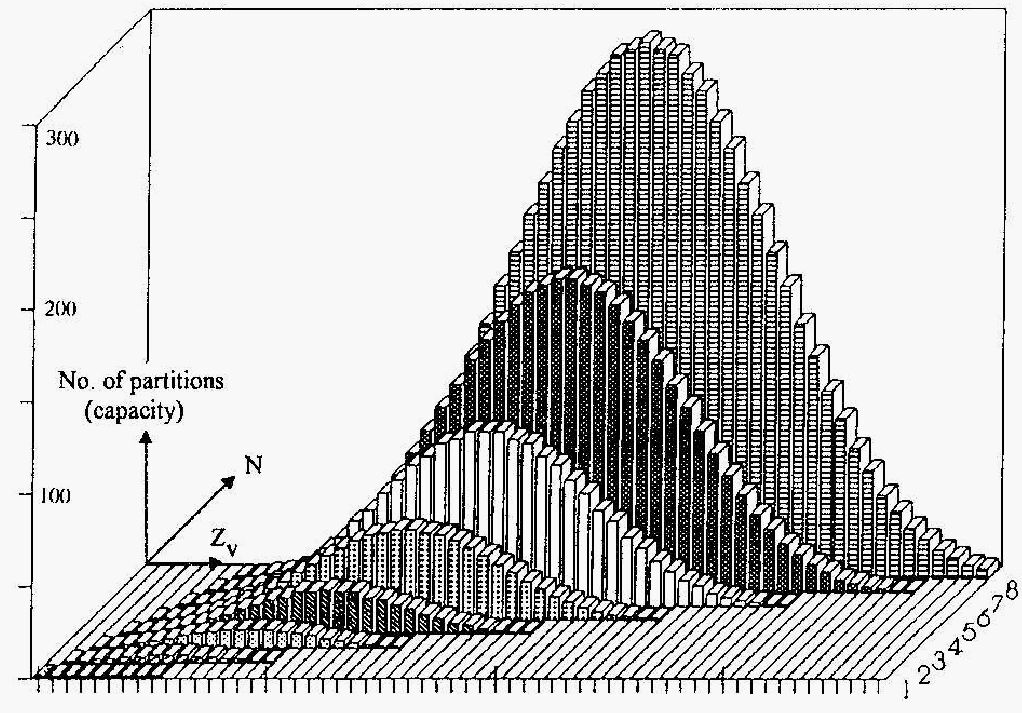
Table of Contents:
I. ORIGIN OF PERIODICITY
II. MENDELEEV PERIODIC TABLE
II.1. What chemists use it for
II.2. How physicists "explain" it
III. PERIODIC SYSTEMS IN OTHER SCIENCES
III.1. Some known criteria for natural systems
III.2. Criteria for periodic systems
III.3. Periodic systems of objects, smaller than atoms
IV. MOLECULAR PERIODICITY
IV.1. How to talk about molecular periodicity
IV.1.A. Local models: examples of diversity
IV.1.B. Early attempts of global classification
IV.1.C. Global models: what to classify and why?
IV.1.D. Atomic periodicity versus molecular?
IV.2. "Nightmares" of global classification and how to avoid them
IV.3. Choice of global similarity parameters: importance of the electron count
V. THE ART AND THE LOGIC OF EQUALIZATION: Classification of isosteric ensembles
V.1. Regularities in the polymorphism of isosteric ensembles
V.2. Chemical trends: the rule of two poles
V.3. Distinguishing between molecules in the PIE
V.4. Topological trends in the PIE
V.4.A. The point on the PIE as a set of molecular pseudographs
V.4.B. Counting of cycles and components from electrons and atoms
V.4.C. Cyclomatic number of pseudograph and homeomorphism of structures
V.4.D. Criteria of connectedness for molecular pseudographs
V.5. Molecular disconnectedness as a hyper-periodic function in the PIE
VI. THE HYPER-PERIODICITY PATTERN: Classification of isovalent ensembles
VII. SPECIAL TYPES OF CHARTS: Diatomic molecules
VIII. CONCLUSION
Acknowledgements
REFERENCESFrom Conclusion:
We may ask, to which branch of exact science we should attribute the art and logic of natural and periodic molecular classifications? Molecules are objects of chemistry and physics, and their classification (as we have seen) requires rather delicate mathematical models. In order to define the appropriate place of such an activity, we may arrange the exact sciences in some sort of a "periodic table":
Physics Chemistry Mathematics Physical Pure&Applied Physics Physical
ChemistryPhysical
MathematicsChemical Chemical
PhysicsPure&Applied Chemistry Chemical
MathematicsMathematical Mathematical
PhysicsMathematical Chemistry Pure&Applied Mathematics The vertical "groups" are pure sciences, while the "rows" are their applications to other sciences. It is easy to see familiar sciences like chemical physics, and physical chemistry, and the branches of applied mathematics. (These terms may be observed, say, as the names of scientific journals, that "periodically" appear in libraries.) We can "predict" two new (still little-known) sciences in the upper-right corner of the table, namely physical and especially chemical mathematics. We may remember that there are relatively new disciplines called chemical topology and chemical graph theory (not with reversed word order), and that these fields are most closely related to the problems discussed in this chapter. It seems that global molecular classifications may be related specifically to chemical mathematics. Let us explain why.
We mean that mathematicians often develop ideal objects and forms without any idea how to apply them to real physical and chemical objects of the Universe. Vice versa, chemists often propose pragmatic, empirical, generalizations about real objects (e.g., homology, isovalency, isomerism, aromaticity, degree of saturation, the octet rule, the repulsion of electron pairs, and so on) without any idea how these concepts relate to one another in a mathematical sense. As we have seen, the interrelation between such archetypal chemical concepts is clearly displayed and clarified in global molecular classifications. Surprisingly, such interrelations appear to have the same nature and the same beauty that exists in rather abstract mathematical objects (homeomorphism of surfaces, connectedness of graphs, properties of partitions, etc.). We can say that we are applying chemistry to mathematics and finding ideal mathematical forms inside chemistry, rather than bringing a mathematical model to chemistry.
More... (to be appeared soon)