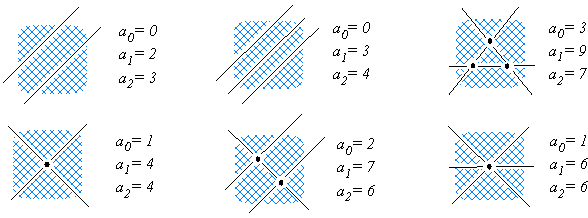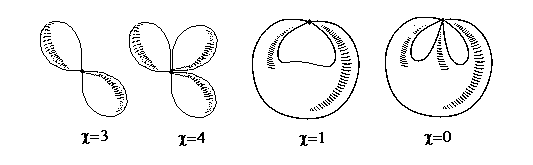Eugene V. Babaev
Moscow State University, Moscow 119899, RUSSIA
1. Introduction
During last two decades, chemistry underwent a strong
influence from nonroutine mathematical methods. Chemical applications of
graph theory [1–10], topology [11–18], and related fields of fundamental
mathematics [21–27] are growing rapidly. This trend may indicate the birth
of a novel interdisciplinary field, mathematical chemistry, imperceptibly
flourishing on the border of chemistry and pure mathematics. The term "chemical
topology" (the title of this volume) has become frequent in papers, books,
and scientific conferences. Similarly, the term molecular topology
(differing in its sense from molecular geometry) has become frequently
used, although there may exist diverse viewpoints on the meaning of this
concept. The key difference between topology and geometry is that in geometry
the concepts of distances and angles are important, whereas in topology
they are not. Instead, the essential topological properties are connectedness
and continuity. Chemical structural formulas are good examples of topological
models of molecules: the pattern of connectivity between atoms is essential,
whereas the interatomic distances and angles are less important and may
be neglected.
A colloquial definition of topology is "rubber" geometry.
Indeed, one may consider a topological object made of an ideal elastic
material, so that any deformation (like stretching or distortion) retains
points of this elastic object "close enough" one to another. In contrast,
cutting separates previously close points, and any joining of parts makes
points "closer" one to another. Such a continuous transformation of an
object without cutting and joining any parts is called homeomorphism.
(The term should not be confused with homomorphism.) The study of properties
that are invariant to homeomorphic transformations is the fundamental goal
of topology. Molecules are nonrigid objects: they may undergo conformational
changes and bond stretching (as evident from molecular spectroscopy) without
deterioration of their integrity. Hence, these "inessential" geometrical
changes of the same molecule may be clearly related to the homeomorphism
[28].
The concept of homeomorphism has one more meaning. It
is not only a change of the same object (to itself), but it is also
a continuous, reversible mapping of one topological object to another.
In other words, it is a sort of a global identification of different
objects. In contrast to the geometrical equivalence of figures (congruency),
topological equivalence (homeomorphism) is a finer and more general relationship.
The homeomorphism differs from isotopy, a manner of embedding of an object
into a space; thus, an ordinary torus and a knotted torus are homeomorphic
but not isotopic. The homeomorphism concept offers a fascinating liberty
of identifying apparently different objects, like a needle and a pipe or
a doughnut and a coffee cup. These objects with quite different geometrical
properties have homeomorphic 2D surfaces, which can be continuously
deformed one to another or to the same surface of a torus. The hole (or
tunnel or cavity) in every one of these objects is preserved upon deformations.
Another, less evident, example of homeomorphism is the equivalence between
a punctured sphere, a hemisphere (with no boundary around the hole), and
a plane. The hole in the hemisphere and the hole (of another type) in the
torus are topological invariants preserved in homeomorphic transformations.
Equality in the number of topological invariants may indicate that the
objects are homeomorphic.
The interpretation of the homeomorphism concept just discussed
may be suitable for chemistry. Equalization of different molecules by arranging
them in series is a long-standing chemical tradition, and periodical and
homological classifications are examples. In these classifications, the
sets of related atoms or structures are grouped together into similarity
classes according to some important numerical invariants (number of valence
electrons, saturation degree, etc.). Are these invariants topological?
Is it possible to treat chemical similarity as a sort of homeomorphism
of molecular models? This aspect of the homeomorphism concept has never
been comprehensively investigated in chemistry, at least as a global phenomenon.
The difficulty is evident: how to relate discrete chemical structures
by continuous mapping? The complementary 2D models of molecules
are apparently more suitable, and there is no difficulty to imagine continuous
mapping of one 2D model to another. However, a serious question
arises, whether the topological invariants of such surfaces are unequivocally
defined. For instance, some fundamental chemical concepts (free radicals,
centers of Lewis basicity and acidity, multiple and multicentered bonds)
are ill-defined in terms of 2D models and even in terms of molecular
graphs.
In the present paper we treat chemical similarity in terms
of the homeomorphism concept and electron count rules. We suggest a novel
interrelationship between molecular graphs and molecular 2D surfaces
by direct mapping of chemical structures (like the Lewis dot formulas)
to the specific 2D manifolds and pseudomanifolds. We define this
mapping in such a way that the lone pairs, free radical centers, and multiple
and multicentered bonds serve as the intrinsic topological invariants of
the 2D models. This approach (a generalization of our earlier works
[29-33]) allows us to apply the homeomorphism concept to chemical problems
in a new way, classifying molecular structures and reactions from the viewpoint
of the topology of surfaces.
The structure of the paper is the following. Section 2
recalls several concepts of the graph theory and topology of surfaces,
necessary for further discussion, and Section 3 is the overview of the
common types of molecular graphs and molecular surfaces used in chemistry.
In Section 4 we treat the concepts of free radicals, lone pairs, and multiple
bonds as intuitively topological concepts, whereas Section 5 provides
an explicit definition and visualization of their topology on the graph-theoretical
level. In Section 6 we suggest an explicit mathematical concept of molecular
topoid, which visualizes the lone pairs, free radicals, and multiple
bonds as sorts of "holes" in an appropriate 2D surface. The topoid
(a "rubber 2D molecule" without geometry) is a novel combinatorial
2D image of molecule, intermediate between ordinary surfaces and
graphs. Operations on topoids (resembling cut-and-paste operations of a
topologist with imaginary 2D manifolds) reflect the key types of
formation and cleavage of chemical bonds. In Section 7 we suggest a novel
conservation law, the invariance of Euler characteristic of molecular topoids,
and use it for classifying the chemical reactions. Section 8 has the goal
to illustrate, how the homeomorphism of topoids brings together diverse
molecular similarity types in a unique manner. In Section 9 we prove that
the explicit 2D image of a graph should be a surface with embedded
Jordan curves, and in Section 10 the nonequivalent types of embedding are
used to expand the common principles of 2D modeling in chemistry.
In Section 11 we use the generalized concept of hypertopoids to
classify the structure and reactivity of molecules with multicentered and
delocalized bonds on the 2D level. Finally, in Section 12 we investigate
the possibility of 2D modeling of the excited states of molecules
with several unpaired electrons by using nonorientable surfaces.
2. Some Useful Concepts of Visual Topology
Expecting that the audience of the readers will be diverse
(and may equally include chemists and topologists), the author provides
an elementary introduction into the concepts of graph theory and of the
topology of surfaces. A mathematician may ignore this section and go directly
to the Section 3, whereas a chemist is advised to accept some important
topological terms and concepts presented below, because they are necessary
in our further discussion. Considering the tradition of visual topology
useful in education [34-37], we substitute (wherever possible) the complex
algebraic expressions by visual images. As Hermann Weyl stated, "The angel
of topology and the devil of abstract algebra fight for the soul of every
individual discipline", and we may add to this, "the angel of visual
topology". More advanced discussions may be found in handbooks on graph
theory [38-41], topology of surfaces [41-46], and general topology courses
[46-49].
2.1. Graphs
A graph may be treated either as an abstract or
a topological object. An abstract graph G is an ordered pair (V,E), where
V is nonempty set of elements (vertices) and E is a set of pairs
of vertices, called edges. In the topological sense, a graph is a finite
set of V points (vertices) connected by E edges (represented as curved
uncrossed arcs homeomorphic to a closed interval). Any graph may be embedded
in the space R3 so that its edges are not self-crossed, although
this may not always be possible for a graph embedded in the plane. A multigraph
has several edges between a pair of vertices. A loop is a specific
curved edge adjacent to the same vertex, and a pseudograph is a
multigraph with loops, (Figure 1).
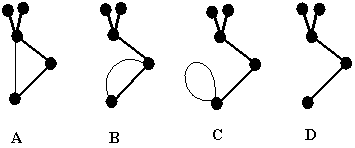
Figure 1. Examples of graph (A), multigraph (B), and pseudograph
(C) with cyclomatic number C = 1. Removal of a cyclic edge results in a
tree (D). All four diagrams together form a single disconnected pseudograph
having 4 components and 3 cycles.
The degree of vertex vi (denoted as
deg vi) is the number of edges adjacent to this vertex; each
loop adds 2 to the degree of the vertex. Therefore, the sum of degrees
of vertices is twice the number of all edges (including loops):
(1) S deg vi = 2
E
A graph may be connected or disconnected
(consisting of K components). A cycle is a closed path in the graph
(a sequence of edges ending with the initial vertex). A cycle in a graph
is homeomorphic to a circle. A loop is also a cycle of unit size, and the
simplest multiple edge (two edges joining two vertices) forms a cycle of
size two. A graph without cycles is a tree. The cyclomatic number
C of a connected graph is the integer:
(2) C = E - V +1,
The value C is not the total number of cycles one may
find in a graph, rather it is the number of independent cycles.
(If C edges are removed step-by-step keeping the intermediate graph(s)
connected, the remainder is a tree.) The cyclomatic number is an additive
property, and for the set of disconnected graphs with K components and
total C cycles (see Figure 1) formula (2) may be rewritten as (3):
(3) C = E - V + K
Graphs are isomorphic if there is a one-to-one
correspondence between their vertices, edges, and adjacencies of vertices.
Graphs may also be homeomorphic. To obtain a homeomorphic graph,
subdivide any edge of a graph by a vertex (giving rise to pair of adjacent
edges) or shrink (if possible) two edges adjacent to a vertex of degree
2 to a new edge.
In a bipartite graph, vertices may be labeled by
two colors, so that no vertices of the same color are adjacent. The colors
of vertices in a bipartite graph alternate, therefore, the cycles are of
even size only. Any graph can be converted to a certain bipartite graph
by a (homeomorphic) subdivision of every edge by a vertex.
2.2. Hypergraphs
The concept of the hypergraph, a generalization
of the graph concept, was introduced in 1970s by Berge [50] and Zykov [51].
A hypergraph is a pair (V, E) of vertices and (hyper)edges, where a hyperedge
is any subset (not only a pair, as in a graph) of the set of vertices V.
The hypergraph H(V,E,R) has an incidentor R(V,E), that assigns adjacency
of a vertex to an edge. Hence, in hypergraphs not only several edges may
be adjacent to the same vertex (as in pseudographs), but also any number
of vertices (not only two, as in a graph) may be adjacent to the same edge.
Any hypergraph has the König representation by a usual bipartite graph
(a König graph) with two colors standing for vertices and hyperedges
of the hypergraph. A hypergraph has a planar representation (Figure 2A),
where a hyperedge is homeomorphic to a bounded 2D disk containing
incident vertices. The adjacency of hyperedges is an overlapping of two
disks in the neighborhood of a vertex (Figure 2A).
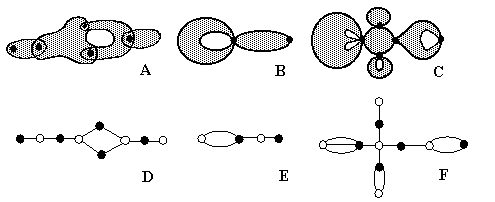
Figure 2. (A) Example of a hypergraph; (B) Example of
a pseudograph (with edges represented by 2D disks) treated as a
pseudo-hypergraph graph. (C) Example of a pseudo-hypergraph with three
different hyperloops and one terminal hyperedge. (D), (E), (F): Representation
of (pseudo)hypergraphs for cases (A), (B), (C) by bipartite graphs (König
graphs). Black color is used for vertices in (A) -- (F). Vertices of white
color in (D), (E), (F) represent images for hyperedges and hyperloops in
(A), (B), (C).
It is possible to assign a cyclomatic number to a hypergraph
(either to its planar representation or to the corresponding König
graph). However, this concept has a serious limitation in respect of considering
pseudographs with loops as particular cases of hypergraphs. The possibility
of the existence of loops in hypergraphs is completely ignored [50,51],
and the only suitable analog of a loop is a "terminal" edge. Let us assume
that the adjacency of two disks (hyperedges) occurs precisely at one point,
which coincide with a vertex. Then it is possible to imagine a "self-incident"
hyperedge (a hyperloop) as a deformed disk mutually adjacent to
the same vertex. A simple example is shown in Figure 2B; here the "usual"
pseudograph is drawn as a planar hypergraph with edges substituted by deformed
disks. Hence, the concept of hypergraphs may be further generalized, and
let us call a hypergraph with hyperloops a pseudo-hypergraph. This
concept (introduced by the present author in 1987 [32]) opens the possibility
of counting cycles (including hyperloops) using an analog of formula (3)
for graphs. Of course, a self-touching hyperloop is also homeomorphic to
a disk (as usual hyperedge), but it has "holes" (degenerate cycles) and
cannot be shrunk into a terminal edge. By contrast to usual edges and loops
(in pseudographs), a hyperloop may serve as an edge, multiple edge, and
a loop in the same time. The König graph of a pseudo-hypergraph should
have multiple edges (Figure 2F).
2.3. Surfaces
A closed 2D surface is an example of connected
2D manifold. Generally, an n-dimensional manifold is a (Hausdorff)
space, such that the neighborhood of every point is homeomorphic to an
open n-dimensional disk. Thus, an object is a 2D-manifolds if an
imaginary 2D disk can be drawn around any point. Such a disk
can be further deformed to a planar disk, and therefore, a closed 2D
surface (2D manifold) is "locally flat" in all its points. Examples
of closed connected surfaces are a sphere and a torus, as well as
a sphere with any number of pasted handles (like surfaces of a pretzel
or a rotary telephone disk). These surfaces are orientable, since
one may define an orientation in 2D neighborhood of a point, consider
a closed path of this point around the surface, and prove that initial
orientation is preserved. The well-known theorem states that the total
set of orientable closed surfaces is exhausted by the family of spheres
SC with C pasted handles. The number of handles is also known
as the genus of the surface. Some familiar examples of surfaces
are presented in Figure 3.
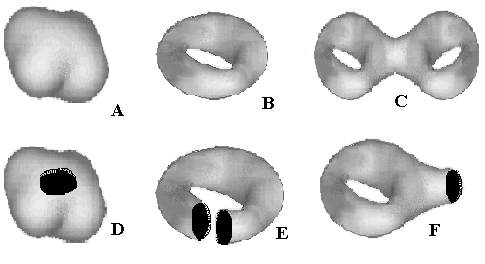
Figure 3. Examples of closed (A, B, C) and open (D, E,
F) orientable 2D surfaces.
A sphere with L punctures or round holes
(LS) is orientable, but it is open (nonclosed) surface. We can
make the puncturing larger by "stretching" the puncture to a hole. The
points on the border of the hole no longer belong to the remaining surface.
The punctured sphere 1S is homeomorphic to a hemisphere (without
equator points), to an open disk (without 1D boundary), and to a
plane, as evident from the stereographic projection of punctured sphere
onto other surfaces. The sphere with two punctures 2S is equivalent
to the cylindrical surface of a tube or to an annulus (of course, without
1D borders).
An operation called the connected sum of surfaces
allows one to construct new surfaces. To visualize this idea, consider
two surfaces, remove a disk (make round hole) in each surface, and connect
disjoint surfaces by pasting a cylindrical tube onto the boundary of each
hole. The number of punctures and handles are additive with respect to
this operation. Thus, mSp#nSq~m+nSp+q
(symbol # designates the connected sum operation, and symbol ~ means homeomorphic).
The genus and punctures of orientable surfaces are numerical
invariants preserved upon topological transformations. Finally, the full
family of compact orientable surfaces (closed or not) with a finite number
of handles and punctures is completely classified by surfaces LSC.
(The canonical form for such a family may be a sphere with C+L holes, of
which C holes are pasted by handles.)
A Möbius band (or Möbius strip), like a cylinder,
is an open surface. However, this is an example of a nonorientable surface
(see Figure 4). The projective plane (4A) and the Klein bottle (Figure
4D) are also nonorientable surfaces, but they are closed in the same sense
as a sphere or a torus. The projective plane is the self-crossed surface
in the R3 space, but not in R4, and it can be also
imagined as the Möbius band (4C) pasted around boundary of a hemisphere.
Therefore, the projective plane may be equivalently drawn as a hemisphere
with pasted "self-crossed cap" (Figure 4B).
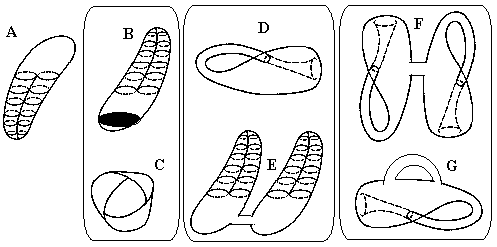
Figure 4. Nonorientable surfaces and their homeomorphisms.
Homeomorphic pairs of surfaces are placed in rectangles.
The Klein bottle is a connected sum of two projective
planes or a sphere with two holes pasted by self-crossed caps (4E). A connected
sum of two Klein bottles (4F) is the Klein bottle with a handle (4G). The
complete family of closed nonorientable surfaces is exhausted by sphere
with L holes each pasted by self-crossed cap.
2.4. Euler Characteristic
The architecture of topological objects may be better
understood in terms of their subdivision (or partition) into cells,
a set of joint "primordial" elements. The en cell is homeomorphic
to an open n-dimensional disk without its (n – 1) boundary, and it is required
that the boundary of a cell in such a partition belongs to the union of
these cells. The e0 cells are points, and the e1
cells are the open intervals (like edges in graphs and polyhedrons with
e0 boundary points removed). The e2 cells are open
disks (like internal parts of polygons without any 1D boundary),
and the e3 cells are open "solid balls" without the 2D
boundary (like a milk inside a carton). Of course, the en cells
are homeomorphic to Rn spaces (line R1, plane R2,
or usual space R3), and the elements from Rn-1 space
may serve as cells for the subdivision of space Rn. For instance,
the usual Cartesian coordinate system (considered as three crossed orthogonal
planes R2) is a subdivision of space R3 into cells.
The most important property of any subdivision into cells
is the alternating sum (4) known as the Euler characteristic c
(4) c = a0 - a1
+
a2 - a3 + ... = S (-1)n
a
n,
where an is the number of en cells.
The value of alternating sum (4) is independent on the number and mutual
arrangement of elements used for subdivision. The simplest example is the
subdivision of a line (space R1) by any number of points: evidently,
a0 points (cells e0) always subdivide a line into
a1 = a0 + 1 segments (cells e1), so that
c(R1)
= - 1. Partitions of a plane by several lines (shown in Figure 5) are more
diverse. However, the value
c remains invariant
either for the case of parallel lines (a0 = 0) or for the case
of lines crossed at any number of points (appearance of e0 cells).
Therefore, c(R2) = 1. For the Cartesian
coordinate system (taken as a partition of space R3) there are:
one cell e0 (center of the coordinate system), six cells e1
(semi-axes from 3 axis), twelve cells e2 (quarters of 3 planes)
and eight cells e3 (octants of space). Finally, c(R3)
= 1 - 6 + 12 - 8 = -1.
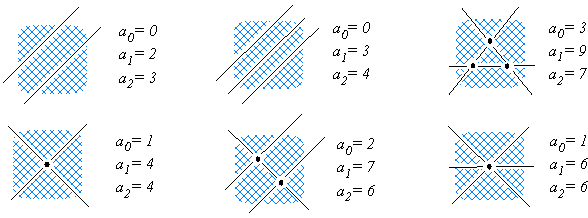
Figure 5. Arrangement of two and three lines on the plane
as different subdivisions of the space R2 (plane) into cells
(e0, e1, e2); ai is the number
of elements ei. The alternating sum c(R2)
= a0 - a1 + a2 = 1 is invariant to the
number and arrangement of lines.
The Euler characteristic is one more intrinsic topological
invariant. A graph consists of only e0 and e1 elements,
and its Euler characteristic is defined by formula (5):
(5) c(G) = a0 -
a1 = V - E = K - C
The Euler characteristic of an orientable closed surface
SC may also be defined in terms of a partition of the surface
into e0, e1, and e2 elements. The simplest
idea of such a partition is the triangulation of a surface. For
instance, consider a hollow tetrahedron or octahedron (with removed faces)
each inside a sphere. A triangulation appears when such a hollow polyhedron
is projected outwards onto the sphere that surrounds it. (Alternatively,
a polyhedron with curved edges may simply be drawn on a surface.) For the
sphere c(S0) = 2, and this result
is the famous Euler theorem:
(6) c(S0) = a0
-
a1 + a2 = V - E + F = 2,
where V, E, and F are the numbers of vertices, edges,
and faces of the convex polyhedron. (The polygons on the faces of a polyhedron
generally may differ from triangles, but may be further triangulated without
changing c.)
The triangulation of a torus S1 results in
c(S1)
= 0. (An example of the torus triangulation is a prismatic block with a
tunnel.) The closed surface SC with C pasted handles has c(SC)
= 2 - 2C. To calculate c for sphere LS
with L punctures or holes, one should consider that some elements (e0
for punctures and e2 for holes) are removed, and the Euler characteristic
is decreased by this value. The presence or absence of the 1D border
around a hole is inessential for calculating of c.
Since this boundary is a circle (with a0 = a1) it
does not contribute to the c value. Therefore,
for a punctured sphere LS (or sphere with holes bounded or not),
c(LS)
= 2 - L. For disconnected sets,
c value is additive
over the set, and the disconnected union of K orientable surfaces {LSC
}K has the following value of
c:
(7) c ({ LSC
}K) = 2 K - 2C - L
The total value of c does not
uniquely characterize the given surface or set of surfaces. There may be
degeneracy in c for nonhomeomorphic connected
surfaces as in the case of a torus or a cylinder, where c
(S1) = c (2S) = 0. Similarly,
the c value of a connected surface may coincide
with that of a disconnected set. Evidently, c
= 2 for a sphere, for a pair of disconnected hemispheres, and for a disjoint
ensemble of a sphere and torus.
A specific type of topological objects is represented
by pseudomanifolds (or wedges of surfaces), where the parts
of different surfaces (or the same surface) are pasted one to another.
The simplest examples of such object are the spaces with base point(s),
like the bouquets of spheres (several spheres joined by only one
point) or a "pinched" torus (a stretched and bent sphere that touches itself
at a single point), see Figure 6.
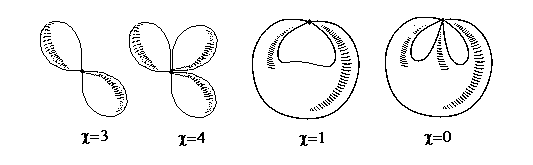
Figure 6. Examples of pseudomanifolds: bouquets of spheres
and self-touching 2D surfaces.
Of course, these objects are not 2D manifolds anymore,
since the neighborhood of a contact point is nonhomeomorphic to a planar
disk. Nevertheless, these complex objects may still be investigated by
the usual methods, e.g., by partitioning them into cells and calculating
their Euler characteristic. For instance, consider removal of the contact
point from the bouquet of k spheres. This operation results in the disjoint
set of k+1 components (one point e0 and k punctured spheres
1S).
Each component has c = 1, therefore, the initial
object has c = k + 1. Note that the value of
c
for any connected and orientable 2D surfaces never exceeds 2 (since
c
(LSC) = 2 - 2C - L). By contrast, the pseudomanifolds
are examples of connected objects with value c
higher than 2.
2.5. Surfaces and Polygons
In some specific cases, a partition of a 2D surface
into cells may consist of unit e2 cell. Thus, a sphere consists
of one cell e2 and one cell e0. A torus consists
of one cell e2, one cell e0, and two cells e1
(crossed meridian and longitude), and. The origin of such an "economical"
partition of a torus becomes clear if we cut the torus along its longitude
and meridian, geting a rectangle with one e2 cell, and then,
restore the same torus by gluing it from the rectangle. Namely, one should
join the opposite sides of a rectangle, obtaining a cylindrical tube, and
subsequently paste the holes of resulting tube to get a torus. Mapping
of a rectangle to a torus (so that some e0 and e1
elements are identified by pasting) is an example of factorization
of a topological object. However, the manner of gluing is essential: twisting
of the same rectangle before gluing results in a Möbius band. Let
us assign vectors to the sides of rectangle (collinear if the sides are
opposite) and call the gluing to be either of "true type" (if collinear
vectors are identified) or of "false type" (if the identified vectors have
opposite directions). Then, the cylinder is constructed by the true-type
gluing, whereas the Möbius band, by the false type. Closed surfaces
may be obtained from rectangle by consecutive "true + true", "true
+ false", and "false + false" types of gluing, and they are
the torus, the Klein bottle, and the projective plane, respectively.
Alternatively, various combinations of vectors may be
placed on the sides of polygons, and only "true-type" gluing (of collinear
vectors) considered (see examples in Figure 7). Generally, the closed and
orientable surface SC may be always obtained from an appropriate
polygon, namely, 4C-gon.
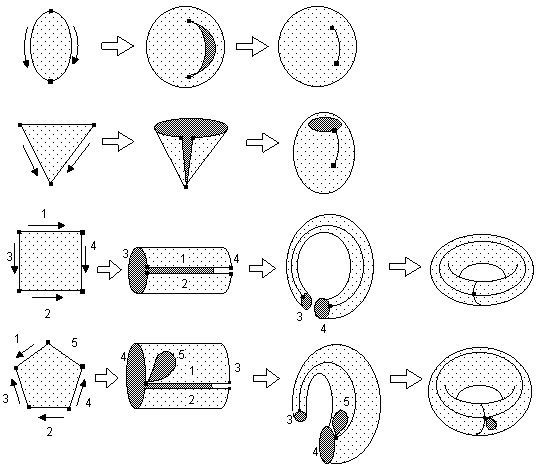
Figure 7. Gluing polygons to orientable surfaces. Numbering
and orientations of the polygon sides prompt which sides should be pasted
to one another (without twisting). Remaining points and lines on the surface
on the right are e0, and e1 cells in partition; e2
cell is shaded).
2.6. Graphs and Surfaces
Usually, the graphs and surfaces are treated as quite
different objects since they consist of different ei elements,
and the cycles of a graph are usually not considered as e2 cells.
An important problem is embedding of a graph on a surface: generally, a
graph may subdivide a surface into regions, and the number of regions depends
on the cyclomatic number of the graph, the genus of the surface, and the
manner of embedding. Thus, a monocyclic graph (e.g., a vertex with
one loop) may subdivide a torus into two regions or not subdivide it at
all. The exact answer exists for the plane: the graph G(V,E) with C cycles
and K components divides the plane into r regions so that r = E - V + K
+ 1 (r = C + 1 for a connected graph). The cycle of a graph is homeomorphic
to a closed curve, and the Jordan theorem states that the closed curve
(Jordan curve) separates the plane (sphere) into two regions. However,
in the general case, the Jordan curve may not subdivide the surface at
all as a single meridian (or a single longitude) does not subdivide a torus.
The coloring of geographic maps on a surface (cf. the famous four-coloring
problem for the plane) is another example where the concept of a graph
is helpful in the topology of surfaces. Here a dual graph is assigned
to a map (vertices represent the regions on a map, and the edges are "roads"
between regions, crossing the borders).
Hence, the common interrelation between graphs and surfaces
is the embedding of a graph on a surface (or simply, it is "a graph on
a surface"). However, there may be another, somewhat paradoxical, interrelation:
"a graph as a surface". This interpretation appears if one tries
to make a model of a topological graph in the real 3D
world, say by drawing it on paper or joining threads or wires. Indeed,
in the real world, where there are no abstract lines (or curves) with zero
thickness, a point drawn in ink is a 2D disk (or even flattened
3D ball), and a thread has a 2D surface homeomorphic to a
sphere. This sort of intuitive mapping is an intriguing mathematical
problem, and the bijective (one-to-one) mapping of a graph to a surface
with Jordan curves will be discussed in Section 9. (This idea, initially
presented by the author in 1986 [52, 53] to an audience of both chemists
and mathematicians, has appeared in late 80s in Russian language handbooks
on graph-theory [40] and topology [49].) An intuitive mapping of graphs
to surfaces is closely related to the principles of modeling in chemistry
(see [54-60] and references therein), since any solid model of a molecular
graph always has 2D surfaces.
Previous Table
of contents Next
Home References