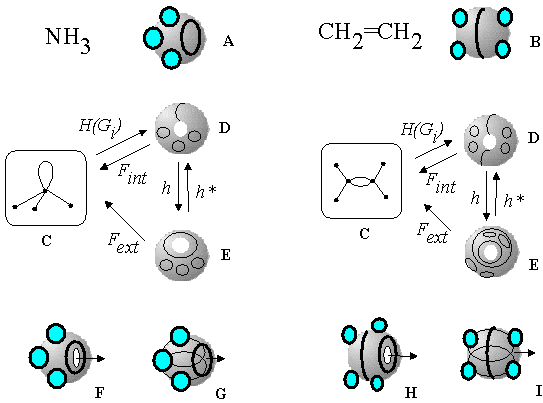Eugene Babaev "Intuitive Chemical Topology Concepts" (c)9. Surfaces with Jordan Curves as Exact Images of Graphs
9.1. Idea and Algorithm of Representing Graph by Labeled Surface
A molecular topoid is a 2D surface with only three invariants (K, L, and C), and from the combinatorial viewpoint, it looks poorer than a molecular graph (graphoid) from which the topoid is obtained. Molecular graph carries a lot of combinatorial information about a molecular structure (connection pattern, isomorphism, size of cycles, branching), whereas in molecular topoids all these features are totally lost. Can this information be reflected in topoids? The question may be reformulated as a quite general and purely mathematical: how to display the adjacency of e0 and e1 elements of a graph (manifested for instance in the incidence matrix of a graph) by any manner on (in) a 2D surface?
As we mentioned above (see Section 2.6) this question is rarely (if ever) appeared in topology. Instead, only the inverse problem ("graph-on-surface") is usually considered, that is, how to assign a graph (e.g., a dual graph) to a labeled surface (e.g., a colored map). Of course, we may place any sort of labels on a 2D surface in order to represent adjacency of vertices of a graph, however it is required that two nonisomorphic graphs have differently labeled surfaces. What might play the role of these labels? As we repeatedly mentioned, an intuitive one-to-one correspondence between graphs and surfaces ("graph-as-surface") is implied in chemical modeling. Thus, in the classical solid space-filling models every atom is represented by a colored solid ball (which is an image of a vertex in a graph), and the bond (image of an edge of a graph) is visualized on a 2D surface as a circumference, which is an area of contact of two colored balls. Therefore, circumferences on a 2D surface are suitable labels for edges of a graph, and any abstract graph (with the cyclomatic number C) intuitively is a set of circumferences drawn on the surface Sc. Each circumference (Jordan curve) is the image of an edge, and the appeared 2D regions symbolize the vertices.
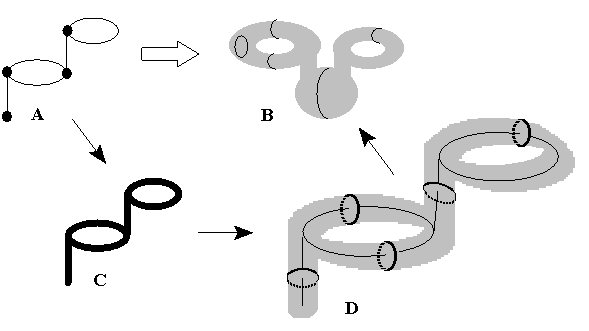
Let us define more precisely how to represent a pseudograph G by a surface labeled by Jordan curves. Let G be a pseudograph with E edges and cyclomatic number C. Create a tubular neighborhood N(G) of G by an adding a ball around every vertex and a solid cylinder around every edge. (The balls and cylinders we add should be "small enough" to preserve all cycles of G from occasional disappearance.) Let SC denote the boundary of N(G). Then, SC is a closed orientable surface of genus C. Now, in each of the solid cylinders in N(G), choose a meridional disk, and let J denote the set of all of the boundaries of these meridional disks. Thus, J is a collection of circles in SC. Let Sic = (SC,J), which is the surface SC together with the collection of circles J. Since every meridional disk matches exactly one edge and J = E, the above procedure unequivocally assigns unique labeling of a surface Sic = (SC,J) to the graph G. Lest there be any doubt on where to locate a meridional disk, put it "in the middle" of an edge, or subdivide every edge by a new vertex (to get a bipartite graph) and build the disks at the places of new points. The overall procedure is visualized in Figure 25. Let us write H(G) = SCi, if the labeled surface is assigned to a graph by the just discussed algorithm H, that we shall call the canonical algorithm.
It should be underlined, that the canonical algorithm H is equally applicable for mapping a graphoid (with some e0 elements absent) to an open orientable surface (LSC, J) labeled by Jordan curves. The difference is trivial: holes should be regarded as specific 2D regions, hence the borders between a surface and the holes are some special sort of Jordan curves. (For assignment of a surface LSC to a graphoid see Section 5.2.)
9.2. Dual Graphs for Labeled Surface
Consider a labeled surface SCi and put a question inversed to just discussed. How to assign a graph dual to this surface, requiring that Jordan curves are prototypes of edges? There may be two types of dual graphs.
Figure 25. Canonical algorithm of mapping a pseudograph (A) to a surface labeled by Jordan curves (B). Intermediate steps: tubular 3D neighborhood of a graph (C) and addition of meridional disks (D) as the images of edges.
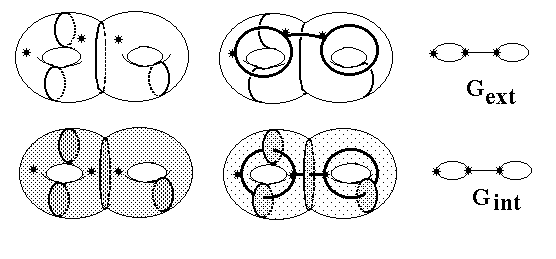
The first graph Gext (externally dual graph) is defined as follows: put one vertex in each 2D region of SCi and connect vertices only if a path from one vertex to another crosses a 1D Jordan curve between the regions. The reconstruction (restoring) of the edge from a torus with meridian gives a loop. The total procedure (shown in Figure 26, top) will be written as Fext(SCi) = Gext, and it resembles drawing of dual graphs for (geographical) maps.
Figure 26. Visualization of two types of dual graphs that can be assigned to a labeled surface. Top: externally dual graph (on the surface). Bottom: internally dual graph (inside the surface).
Another dual graph Gint (internally dual graph) is defined by the reversal of the above canonical algorithm in Figure 25. Namely, for each 1D circle on the surface SCi, we should add (if possible) a meridional 2D disk so that the circle becomes the boundary of this disk. (This is not always possible, e.g., in the case of a torus we may place a 2D disk to any meridian, but not to a longitude.) The appearance of disks results in a set of e3 cells bordered by e2 cells (either initial SC or new 2D disks). Now, locate a point (vertex of the Gint graph) inside each e3 cell, and draw an edge only if there is a path from one point to another that crosses the 2D disk. (Whenever the two sides of a nonseparating Jordan curve are the part of the same region, we will create a loop in the graph) The procedure (shown in Figure 26, bottom) will be denoted as Fint(SCi) = Gint. The definition of Gint may illustrate how chemists "see" a molecular graph (atoms connected by bonds) hidden inside the molecular space-filling models.
Above we suggested a method (canonical mapping H) of obtaining a labeled surface from a graph. Now let us check whether the same graph (or a graph isomorphic to the initial one) will be returned back from the labeled surface by the operations Fint and Fext. Evidently, if SCi is obtained from the graph G by the canonical algorithm H(G), the internally dual graph is the same graph G:
(13) Fint [H(G)] ~ G
Here "~" means "isomorphic to", and brackets indicate subsequent action of operations. Hence, the operation Fint restores the same graph.
Less trivial is relation (14):
(14) Fext [H(Gi)] ~ Gi
Nevertheless, it is true, since the canonical algorithm H is so "good" labeling of SCi, that Gint can be continuously deformed to Gext giving the isomorphic graph (see Figure 26).
9.3. Labeled Sphere and Trees
Several circles may be arranged on the surface in either equivalent or nonequivalent manner. Let S denote any surface containing a collection of disjoint circles J1 and another collection of disjoint circles J2, where the sets J1 and J2 may intersect. We define (S,J1) to be equivalent to (S,J2) if there is a homeomorphism h from S to itself such that h(J1) = J2.
Now let Sci = (S0,J) be the sphere labeled (partitioned) by any number of circles in any manner. Then, it is true that:
(15) Fext(S0,J) ~ Fint(S0,J),
(16) H [Fext(S0,J)] = H [Fint(S0,J)] = (S0,J),
Hence, for any labeling of the sphere both types of dual graphs always coincide (expression (15)). Of course, the dual graph here is always a tree. Furthermore, the application of the canonical mapping H to this dual tree restores just the initial arrangement of labels (expression (16)).
THEOREM 1: The number of nonequivalent labeling (partitions) of the sphere by E Jordan
curves is equal to the number of nonisomorphic (and nonrooted) trees with E edges.
The proof elementary follows from expressions (13) -- (16) and the equality J = E.
9.4. Labeled Torus and Monocycles
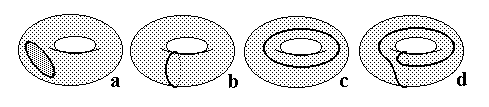
The case of a sphere is unique because any labeling by circles is in the one-to-one correspondence to a certain tree. Generally, a labeled surface may not have a dual graph at all, or the internal dual graph may be absent. This is evident from the cycles a, b, c, and d (Figure 27) drawn on the toroidal surface.
Figure 27. Various possibilities of arrangement (embedding) a closed Jordan curve on the torus (see the text).
Case a is the worst: no dual graph can be assigned to this labeled surface, and this arrangement of a circle on a torus cannot be an image of any graph. Case b is the best: both dual graphs exist and are isomorphic. Cases c, d are intermediate: graph Gext exists but Gint not. Cases b, c, d may be generalized: any closed spiral line on the torus is representable as a "sum" of few longitudes and few meridians nb + mc (n and m are natural numbers showing how many times the fragment of spiral "resembles" meridian b and longitude c). Then b = 1b + 0c, c = 0b + 1c, d = 1b + 1c.
Let us say the labeling of a torus is perfect if at least one closed cycle is different from the cycle a. Let us say, the labeling of the torus belongs to the same (n,m) class if it is perfect and if at least one circle used for labeling is of nb+mc type, where b is a meridian and c is a longitude. Let us write this labeling as (Tn,m,J), where J is a set of closed curves. Then, for any (T1,0,J) labeling of the torus by any number and any arrangement of circles it is evident that:
(17) Fext(T1,0, J) ~ Fint(T1,0, J),
(18) H [Fext(T1,0,J)] = H [Fint(T1,0,J)] = (T1,0, J)
Hence, for any (0,1) class of labeling of the torus (perfect and by at least one meridian) both dual graphs, external and internal, coincide (expression (17)). Of course, such dual graph is always a monocyclic graph (maybe with a loop or a multiple edge). Furthermore, the application of the canonical procedure H to this dual graph restores just the initial arrangement of labels (T1,0, J) (expression (18)).
We may conclude that the (0,1) class of labeling of the torus is the best, because it is the same as for the sphere, and therefore, within this class we may freely switch from graphs to surfaces (operation H) and back (using either of two operation, Fext or Fint). This seems impossible for other (m,n) classes, where the operation Fext is defined but Fint is not. Nevertheless, there are some homeomorphisms on the torus that take any nb+mc curve to the meridian 1b+0c, or, in other words, any "bad" (m,n) class of labeling to a "good" (1,0) class. For instance, we may always invert a torus with longitude(s) to a torus with meridian(s), changing a labeling from (0,1) to (1,0) class (Figure 28).
Figure 28. Labeling of a torus from the (0,1) class (left) and from the (1,0) class (right). A homeomorphism h(T0,1,J) = (T1,0,J) that transforms the left object to the right one is the inversion of a torus with Jordan curves.
By other words, there is a homeomorphism h: h(T0,1,J) = (T1,0, K) = (T1,0, J). The operation h opens the possibility of extracting the Gext graphs (which are isomorphic to the initial graph G) "indirectly" from the class where they are impossible. Such a homeomorphism (although less visual) of a torus to itself is possible for any Tm,n, and let us state that h(Tm,n,J) = (T1,0, K) = (T1,0, J). Therefore:
(19) Fext (Tm,n,J) ~ Fint (T1,0,J)
(20) H [Fext(Tm,n)] = H [Fint(T1,0)] = T1,0
THEOREM 2: The number of nonequivalent labeling (partitions) of the torus by E Jordan
curves within each Tm,n class is equal to the number of nonisomorphic
monocyclic pseudographs with E edges.
The proof is evident, because for the good class (T1,0) each pseudograph is in the one-to-one correspondence to a certain labeled torus, and any labeling (Tm,n,J) from "bad" class may be reduced to a good class by a homeomorphism h.
The question arises, whether the relationships similar to the just discussed exist for the surfaces with more than one handle? Even for the case of pretzel the picture is unclear, and the author offers this problem for professional topologists.*) Anyway, expressions (13) and (14) are true for C > 1.
*) Very recently E. Flapan (Los Angeles) stated [129] that the following theorem is true:Let C be any fixed positive integer. For a given surface S of genus C, let Qi denote any finite set of disjoint simple closed curves contained in S which has the property that if we cut S open along all of the curves in the set Qi, then we will obtain a collection of planar surfaces. We will say two such collections Qi and Qj are equivalent if there is a homeomorphism h from S to itself such that h(Qi) = Qj. Let Q denote the set of all equivalence classes of such collections of curves. Let P denote the set of all pseudographs with cyclomatic number C. Then there is a bijection between Q and P.
10. Chemical Applications of Surfaces with Embedded Jordan Curves
The theorems proved in the previous section may be useful in the general methodology of molecular 2D modeling. First, the chemical problems related to the isomorphism of graphs (e.g., the chemical isomerism) may be translated to the language of equivalent and nonequivalent embedding the Jordan curves on a 2D surface. Second, the problem of 2D visualization of a lone pair and multiple bond (still poorly or even contradictorily resolved in common models) may get an explicit mathematical answer. Third, an intriguing expansion of the common principles of 2D molecular modelling may be suggested for the cyclic molecules with the delocalized bonds.
10.1. Chemical Isomerism and Homology: a Novel Viewpoint
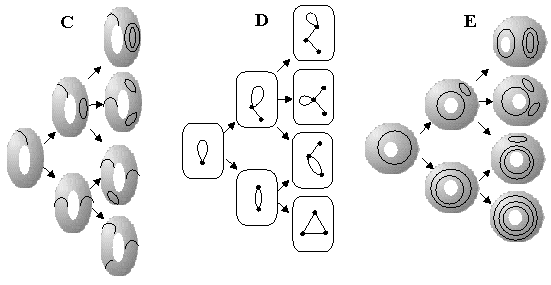
A unique parallelism between trees and a labeled sphere (Theorem 1) relates the fundamental problem of chemical isomerism in saturated hydrocarbons (usually treated only at the level of graphs) to the problem of nonequivalent arrangements of Jordan curves on a sphere. To make this statement clear, consider hydrogen-suppressed graphs of alkanes. Let us represent the family of these graphs by the set of labeled spheres. Let us draw an arrow between two labeled spheres only if an addition of one Jordan curve to a labeling (S0,J)m results in a labeling (S0,J+1)n (see Figure 29 A). Because each labeling (S0,J)n corresponds to a unique tree, let us shift from the set of surfaces to the set of trees, keeping the set of arrows the same (Figure 29 B). Now a novel relationship (manifested by the set of arrows) appears between the trees with V vertices and V+1 vertices. From the chemical viewpoint, Figure 29 B represents a combinatorial relationship between the structures of alkanes, namely, between their higher and lower homologues (graphs joined by an arrow) and isomers (graphs on the same level of the diagram). However, this relationship follows only from the topologyof surfaces, and it does not follow from the graph theory.
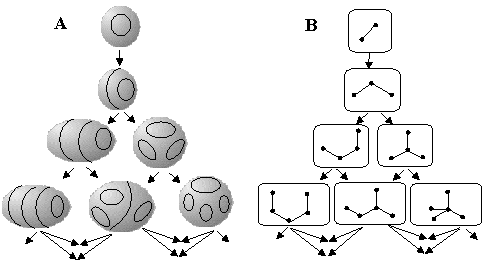
Figure 29. An illustration of one-by-one addition of circles (Jordan curves) to a sphere (A) and a torus (C and E). An arrow shows the possibility to obtain a novel labeling of a surface by placing a circle to the previous labeling. The same type of relationship is shown for the the dual graphs of labeled surfaces, trees (B) and monocyclic pseudographs (D).
The old problem of chemical enumeration (e.g., of isomers and CH2 homologues) frequently implies the application of the orbits of a graph automorphism group [1, 2, 8, 130] (defined on the permutation of vertices or edges). A labeled surface is another combinatorial object with another type of the "automorphism group". The further discussion is beyond the scope of this paper, and our goal is only to underline the existence (and importance) of this problem. In Figure 29 C -- E the same -- novel -- type of relationship (consequence from Theorem 2) is shown for the families of 2D objects (from T1,0 and T0,1 classes) and the corresponding monocyclic pseudographs. If the labeled surfaces represent usual molecular pseudographs (not only hydrogen-suppressed graphs), then nonequivalent arrangements of J curves equally cover isomers, ylides, betaines, or resonance structures with heteroatoms. Therefore, isomerism and isosterism become indistinguishable from the combinatorial viewpoint.
10.2. Homeomorphism and Isotopy: Lone Pair and Double Bond
As mentioned in Section 3, the relationship between structural formulas drawn on paper and some classical 2D models is usually considered as a simple one-to-one correspondence. Upon careful inspection, this relationship appears not so simple (Sections 5 -- 8), and the correspondence, from the topological viewpoint, may not be one-to-one (see Section 9). Fortunately, the manner in which chemists construct various 2D models (e.g., space-filling and ball-and-stick models) from structural formulas resembles canonical mapping H. Indeed, in most 2D models of cyclic molecules (say, of saturated hydrocarbons CnH2n+x) it is always possible to place a meridional disk between the positions of two atoms, former vertices of a graph. There may be a disk between adjacent balls in the space-filling 2D models, or a disk across a "stick" in the ball-and-stick models. Therefore, an intuitive one-to-one correspondence (molecular graphs -- classical molecular 2D surfaces) may be explicitly confirmed. The expanded one-to-one correspondence between molecular graphoids and molecular topoids (involving free radicals, multiple bonds, and lone pairs) is, of course, also possible. Equations (13) – (18) prove this, and the structural formula (molecular graph, multigraph, pseudograph, or graphoid) represented as a 2D model may be unequivocally reconstructed (returned back unchanged) as a dual graph of any type, either external or internal.
Nevertheless, the canonical mapping of a molecular graph to a labeled surface does not exhaust all strategies of topological design at 2D level of molecular modeling. Equations (19), (20) indicate that for cyclic molecules, it is possible to assign more than one 2D model, which will be in the one-to-one correspondence one to another and to the parent molecular graph. For instance, the toroidal 2D model of a monocyclic molecule may have the arrangement of Jordan curves from any (m,n) class. Let us apply this idea to represent a double bond and a lone pair, the simplest cycles in molecular pseudographs, and the worst cases of molecular 2D modeling (see Section 4). Both features are frequently represented by a single circle (Jordan curve) on a spherical surface (see Figure 30 A, B). In the case of ammonia (Figure 30A), such a circle helps to represent the most compact arrangement of bonding and nonbonding electron pairs (as a set of circles on a sphere) in order to predict molecular geometry [97, 98]. In the case of ethylene (Figure 30 B), a circle represents a single interaction of two VDW spheres along the C=C bond.
Figure 30. Various 2D models of NH3 (left) and C2H4 (right); Jordan curves on surfaces represent electron pairs. Standard 2D model of NH3 (A) and C2H4 (B) with a single Jordan curve on a sphere. Molecular pseudographs (C) and their toroidal topoids with meridians (D) and longitudes (E) representing the edges of the parent graphs. The surfaces with longitudes and visible holes (F,H) may be self-crossed (G, I).
Within the model of labeled topoids this picture is changed. Of course, the surfaces of NH3 and C2H4 are toroidal with one circle for a lone pair and two circles for a double bond. For each case, the corresponding molecular pseudograph Gi (Figure 30 C) may be transformed either to a surface with meridian(s) (Figure 30 D) or to a surface with longitude(s) (Figure 30 E) by applying the canonical mapping H(Gi) = (T1,0, J) and the homeomorphism h(T1,0,J) = (T0,1,J). For each molecule, the models D and E (Figure 30) are homeomorphic, but not isotopic. The initial monocyclic graph Gi may be unequivocally restored from these 2D models by different ways (see Section 9), directly (D to C or E to C) or indirectly (considering the homeomorphisms h and h* between D and E).
As mentioned above (Section 6.3), the most logical 2D image of a lone pair (and of a double bond) is a "pseudo-spherical" surface with the masked hole (self-crossed torus). The self-crossed surfaces with longitudes (G and I) have some advantages over the models with meridians. Only the longitudes (not the meridians) are equally visible in both self-crossed and normal toroidal surfaces (cf. cases F and G or H and I in Figure 30). The self-crossed model of ammonia with a longitude (Figure 30 G), resembling the common model (Figure 30 A), allows a symmetrical arrangement of the circles (electron pairs) around the surface and may, therefore, predict the same geometry type of NH3 as does the VSEPR model. Furthermore, in the model G (Figure 30), the longitude may be continuously shifted throughout the invisible self-crossed part, illustrating well-known phenomenon of the pyramidal ammonia inversion. Similarly, the model of C2H4 with two longitudes (E) is more preferable than the model with meridians (D). The first one (model H in Figure 30), being changed to the self-crossed image (Figure 30 I), has only one longitude on the external surface (and one more inside). The model in Figure 30 I resembles the standard space-filling model of C2H4 (Figure 30 B). Furthermore, the elliptical self-crossed region inside the double bond (the trace of a hole) is located along the axis C-C in complete agreement with the model of Bader. Finally, any difference in the isotopy of the discussed 2D models in R3 (presence of usual or masked hole, drawing a circle as a meridian or as a longitude) is compensated by their topological indistinguishability (at least, in space R4). Therefore, an inessential difference may be removed by an appropriate homeomorphism.
10.3. Isotopy and Delocalization in Cycles
The substitution of one Tm,n class by another, possible for cyclic molecules, may be interesting for the case of conjugated chains and cycles. An alternating sequence of single and double bonds (along a chain or around a planar cycle) results in essential delocalization of double bonds. Expression of this phenomenon is impossible in terms of common molecular models. In a molecular graph, the position of a single or a multiple edge is strictly fixed. Similarly, in conventional 2D models the position of a single meridional Jordan curve (or two curves) is localized in the specific 2D region. However, a homeomorphic change of a labeled 2D model (from T1,0 to T0,1 class) may help to resolve this old paradox of chemical modeling.
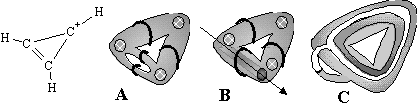
A topoid of a conjugated molecule may have several handles, and each handle has various number of Jordan curves. Consider the simplest example of the delocalized cyclic molecule, the cyclopropenilium cation (Figure 31), that consists of cycles c2 and c3. We may represent the double bond by a toroidal fragment with two meridians (Figure 31 A) or with two longitudes (Figure 31 B). However, the cyclic cation has localized and delocalized bonds, so we may relate the manner of embedding a Jordan curve with the localization of a bond. Let a meridional Jordan curve represents a localized bond. Indeed, one may always add a disk (wall) to such a curve and locate the disk in a certain position bounding the nuclei inside the surface. Now assume that the Jordan curve homeomorphic to a longitude of a torus represents a delocalized bond. This also makes sense: a longitude (image of a bond) rounds the 2D toroidal surface with nuclei inside. Hence, for the cyclopropenilium cation we may draw three longitudes rounding the "large" hole (cycle c3) and one meridian across the additional "small" hole (Figure 31 C). This picture is parallel to the concept of s-delocalization in the aromatic systems, recently discussed in quantum-chemistry [131, 132].
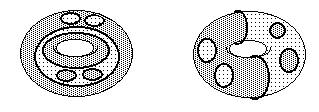
Figure 31. Various arrangement of Jordan curves on the surface of pretzel representing C-C bonds in 2D models of the cyclopropenilium cation. (A) Four meridians. (B) Two meridians and two longitudes; an arrow indicates the arrangement of the second hole with one more longitude inside. (C) Three longitudes and one meridian (circles for the hydrogen atoms are not shown).
In general case, the topoid of a conjugated molecule with several handles may have various types of Jordan curves: some of them are "meridian-like" and other may be "longitude-like". The benzene molecule may be represented as a topoid with six longitudes and three meridians (or vice versa). Clearly, a graph Gi that may be reconstructed from these 2D models (directly by the operation Fext or indirectly by the combination of operation Fint with the homeomorphism h*), is the parent molecular graph Gi (like a single Kekule formula of benzene).