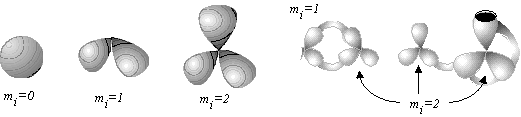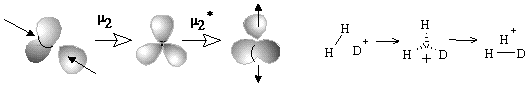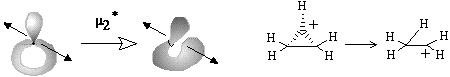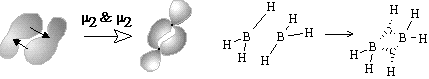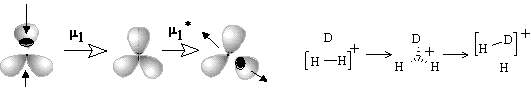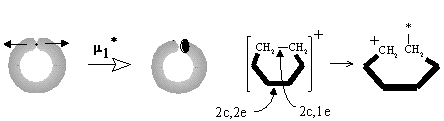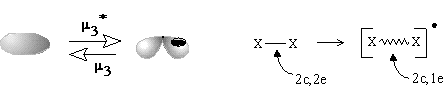Eugene Babaev "Intuitive Chemical Topology Concepts" (c)11. Delocalized Bonds and Hypertopoids
There are a lot of molecules to which it is impossible to assign certain molecular structure with localized two-centered and two-electron (2c,2e) bonds and, hence, to draw a certain molecular graph. The reasons may be different. For example, there may be violation of habitual valency of an atom (e.g., of the hydrogen atom in the hydrogen bonds X-H-X or of the carbon atom in transition states X-CR3-Y of SN2 reactions). Another reason is the delocalization of free electrons, lone pairs, and double bonds, manifested for instance, in the appearance of unexpectedly higher symmetry of a molecule (benzene, charged or radical allyl system, nonclassical cations) or in an abnormal length of single and double bonds (conjugated dyes). Finally, there may be a deficiency of edges (2c,2e-bonds) necessary for forming a connected graph (like in H3+, CH5+, boron hydrides), so that the structures should be discussed only in terms of three-centered and two-electron (3c,2e) bonds. Perhaps, the worst cases for molecular modeling are the cation radicals (like H2+ and CH4+) where it may be necessary to assume the existence of two-centered one-electron (2c,1e) bonds.
For these uncertain cases, the conventional structural formulas are frequently drawn with dashed lines, where the concepts of cyclomatic number, connectedness, and homeomorphism become unclear. Any discussion of topology for these cases seems possible only in terms of molecular orbitals or at least the graphs extracted from Ñr analysis of the electron density. Nevertheless, the necessity of storing the structural information about molecules in computer databases, independently on the type of intra- and intermolecular bonds, stimulates attempts to describe delocalized structures in terms of graphs and matrices. [133 -- 135].
11.1. Attempts to Use Molecular Graphs and Hypergraphs
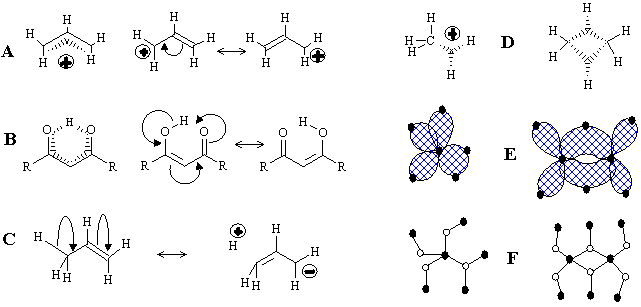
In parallel to the MO pictures (poorly compatible with the traditional concept of bonds) chemists continue developing the combinatorial models related to the molecular graph concept even for the uncertain cases discussed above. The first (and the eldest) model, pioneered by Lapworth, Robinson, and Ingold [136], is the use of curved arrows that complement molecular graphs (Figure 32 A -- C). The arrows indicate a topological feature (free radical, lone pair, or a single/multiple bond) to be selected and rearranged in the molecular graph. Evidently, this approach is combinatorial because the entities and their number are exactly indicated, and the "fortune" of each entity is predetermined by an arrow. Finally, an uncertain delocalized structure is assumed to lie in-between certain graphs (resonance forms) with exact cyclomatic numbers and connectedness. The resonance forms may be isomorphic (as in examples on Scheme 32 A, B), nonisomorphic (as in conjugated cyanine dyes), or even disconnected graph (like in the boundary structure in Figure 32 C for the hyperconjugation of a CH3 group). The qualitative combinatorial picture of a molecule as a set of resonance structures becomes quantitative in the formalism of valence bonds theory [91].
Figure 32. Various topological representation of molecules with delocalized bonds. (A) Delocalization in the allyl cation. (B) An example of the intramolecular hydrogen bond. (C) The hyperconjugation in propene illustrated by the disconnected resonance formula. (D) The standard representation of molecules CH5+ and B2H6 with (3c,2e) bonds; (E) the same structures represented by hypergraphs (with bonds as planar 2D disks) and corresponding König graphs (F).
Another concept, also related to graph theory, is the formalism of depicting (3c,2e) bond by adding specific subgraphs adjacent to the localized (2c,2e) skeletal framework. Thus, the (3c,2e) bond may be regarded to as a specific vertex of degree 3 (the image of a bond, not of an atom) connected by dashed edges to three atoms participating in the multicentered bonding (Figure 32 D). The models originate from the so called styx-formulas suggested by Lipscomb for the structures of boron hydrides [123]. (The letters s, t, y, x initially denoted different types of (2c,2e) and (3c,2e) bonds in boranes.) The styx-formulas were generalized [137], reviewed [111], and extensively used by Olah and others to describe the topology of hypervalent electron-deficient molecules and clusters. In such "molecular graphs", vertices have two types of labels (one for atoms and another for (3c,2e) bonds) and two types of labeled edges, usual (for (2c,2e) bonds) and dashed (joining differently labeled vertices). We may conclude that the styx-formula is an intuitive application of the hypergraph concept for molecular modeling (see Figure 32 E). Indeed, the common styx-formulas with (3c,2e) bonds (like in Figure 32 D) resemble an incomplete König representation for hypergraphs (Figure 32 F), because usual (2c,2e) bonds are still drawn as edges, not vertices. Understanding of this fact [32] was fruitful and led to the development of topological indices of molecular hypergraphs and algorithms for storing the data on delocalized structures in computer databases [138].
Both concepts discussed above are ill-defined on the level of 2D models. The topological invariants of hypergraphs with (3c,2e) bonds are uncertain at the 2D level. Of course, the König graphs (with definitive cyclomatic number) may be helpful for the development of certain 2D images for molecules with (3c,2e) bonds. However, it is still unclear what type of topological objects should be assigned to the radical cations with (2c,1e) bond (like H2+ and CH4+). Such species and their fragmentation form the central subject of the mass-spectroscopy, where the lack of good structural models is pronounced [139]. Let us prove that the concept of topoids may serve for the rigorous description of (3c,2e) and (2c,1e) bonds as fundamental topological invariants, and the curved arrows of chemists relate to specific topological transformations.
11.2. Pseudomanifolds and Their Euler Characteristic
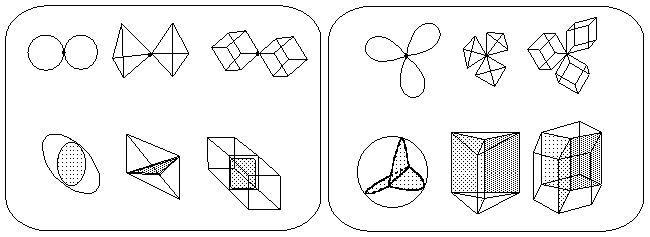
As we mentioned in Section 8, an attempt to calculate the Euler characteristic for topoids of boron hydrides starting from the electron count (2N -- Z = c) leads to c = 4 (nido-class) and c = 6 (arachno-class). Similar calculation for a cation CH5+ (with the 3c,2e-bond) lead to c = 4, and the cation-radical CH4+ (with 2c,1e-bond) has c = 3. These c values are impossible for the closed 2D manifold. Nevertheless, there are a lot of triangulable 2D objects with c>2 that consists of usual topological cells ei. These objects, however, are not the 2D manifolds. They are the pseudomanifolds (see Section 2.4 and Figure 6). The simplest pseudomanifolds are the bouquets of spheres. Let us examine, how these simplest models may relate to molecular topoids, and how one may calculate their Euler characteristic without partition into cells.
A bouquet of spheres (unlike a usual sphere) has a specific point with a neighborhood of this point not homeomorphic to a planar 2D disk. Consider a bouquet of mi+1 spheres (designated as Wmi+1(S0)) attached to the same point. Let us call this point a base point of index mi. The index of a base point (that is, mi) should not be confused with the number of spheres around this point (that is, mi+1); a single sphere S0 (a "bouquet of one sphere" W1(S0)) has index mi = 0 for any point on its surface.
Consider a set of k disjoint bouquets {Wmi+1(S0)}k each with the single base point of index mi. Let M be equal to Smi. The Euler characteristic c for a single bouquet of spheres Wmi+1(S0) and for the disconnected set of k bouquets follows equations (21a) and (21b), respectively.
(21a) c[Wmi+1(S0)] = 2 + mi
(21b) c[{Wmi+1(S0)}k] = 2K + M,
Let us construct more complex objects from a bouquet of spheres. Consider a finite number k of such bouquets and allow making of any number of punctures or holes (except puncturing the base points) and any gluing of the holes together
Figure 33. Indices of the base points in various pseudomanigolds derived from the bouquets of spheres. All diagrams together form a single disconnected pseudomanifold W having K = 5, L = 1, C = 3, M = 10, and c(W) = 13.
(with a restriction to preserve the orientability). Some punctures may be preserved upon the gluing. The result will be the appearance of handles and a change in the number of components k. Of course, the pasting preserves any index mi and the total value M. The resulting object is a (disconnected) pseudomanifold W (see Figure 33). To calculate the Euler characteristic c(W), consider a mapping f(W) = {LSC}K, that takes a pseudomanifold to a usual orientable (may be disconnected) 2D surface {LSC}K. The mapping requires the substitution of "abnormal" k base points by "normal" 2D-fragments. For instance, remove a base point and paste the appeared mi+1 holes by a sphere mi+1S (sphere with mi+1 punctures). The resulting object is the set of orientable surfaces {LSC}K, and let it be exactly K components, C handles, and L punctures. Then the Euler characteristic of the initial pseudomanifold should be (22):
(22a) c(W) = 2K -- 2C -- L + M
The proof is obvious: reverse the mapping f(W) to return back k "abnormal" base points and apply the formula (21b).
11.3. Molecular Hypertopoids and their Homeomorphism
The pseudomanifolds derived from the bouquets of spheres may be helpful as exact topological images of molecules with multicentered bonds. Let us assume that for such 2D models the Euler characteristic satisfies equation c = 2N -- Z (as it was for localized case) and write:
(22b) c(W) = 2K -- 2C -- L + M = 2N -- Z
This hypothesis is very strong: we may have no an a priori knowledge about the mapping of a molecule to a pseudomanifold, however, the electron count is always exact. Therefore, for any uncertain type of chemical bond we may use equation (22b) to "extract" the set of topological invariants (K, C, L, and M) and the 2D model itself! Let us assume that the index of a base point reflects the type of bonding. Thus, for a molecule with usual localized (2c,2e) bonds the value M is equal to zero (because any point on usual 2D surface has index mi = 0). Of course, for this case of bonding, a pseudomanifold is reduced to usual 2D manifold (topoid), and equation (22b) is changed to equation (11b). Let us examine how to extract possible 2D images (pseudomanifolds) for the simplest (3c,2e) and (2c,1e) bonds.
For the simplest molecule H3+ with one multicentered (3c,2e) bond, we have c = 2N -- Z = 6 -- 2 = 4. If the molecule is considered to be connected (K = 1) and has neither cycles nor unpaired electrons (C = L = 0), then M = 2 (M = c -- 2K = 4 -- 2 = 2). The 2D model is assumed to be a pseudomanifold, and M = Smi implies that there may be k base points. Consider k = 1, then the presence of unit base point of index mi = 2 corresponds to the bouquet of three spheres. The resulting mathematical image perfectly matches the known structure of H3+: 2D regions are atoms, and (3c,2e) bond is the base point to which the spheres are attached.
For the simplest cation-radical molecule H2+ we have c = 2N -- Z = 4 -- 1 = 3. Assume, that the molecule has no free radical centers (unlike usual free radicals H or CH3), because here the unpaired electron forms a specific (2c,1e) bond. Therefore, L = 0. If the molecule is again considered connected (K = 1) and without cycles (C = 0), then M = 1 (M = c -- 2K = 3 -- 2 = 1) and the 2D model uniquely corresponds to the bouquet of two spheres. Of course, such topological 2D image of the (2c,1e) bond (two spheres pasted by a point) differs from that of (2c,2e) bond (a tube) and (3c,2e) bonds (three spheres pasted to a point).
Let us call these prototype models molecular hypertopoids. In the previous sections we proved the usefulness of the homeomorphism principle for usual topoids. Let us apply it to hypertopoids. By taking a bouquet of 2 or 3 spheres as the models of H2+ and H3+, we may label the spheres (any one or every one), drawing new Jordan curves on them. A suitable combination of curves may be related to the homeomorphic insertion of specific groups (like CH2, BH or other fragments) without violating the value c. The stepwise addition of Jordan curves symbolizes homological series. The possibility of arranging the same number of curves by various ways is the isomerism. Such a labeling (homeomorphic insertion of CH2 groups) in H3+ cation leads to the homological family of protonated alkanes CnH2n+3+. The parent cation CH5+ (with hypercoordinated carbon atom) and its homologues have the same topological pattern as in the initial molecule H3+ (see Figure 34 A). Homological series of H2+, of course, is the family of radical cations of alkanes CnH2n+2+, (like CH4+). For this series the 2D surface is not smooth; it has a node representing (2c,1e) bond.
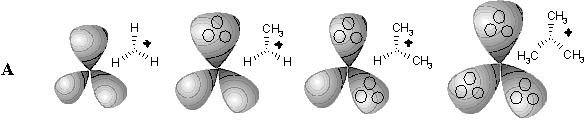
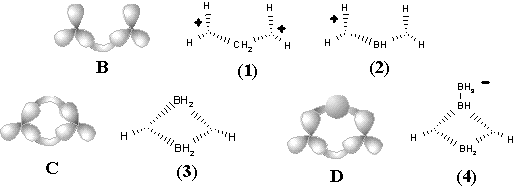

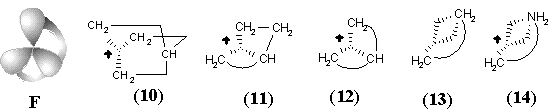
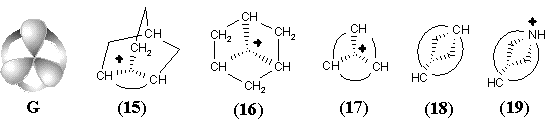
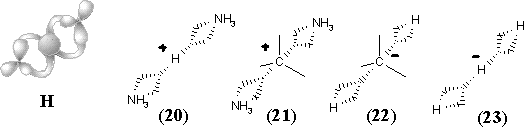
Figure 34. Homeomorphism in hypertopoids (see the text). Standard representation of molecules with multicentered bonds by styx-formulas may be expanded if three ends of (3c,2e) bond (shown by dashed line) are incident to two atoms (as in diagrams (8), (9), (13), (14), (18) -- (23)).
Another familiar topological operation, that may be applied to hypertopoids, is the connected sum. As usual, this operation requires the removal of terminal hydrogen atoms and pasting the appearing pair of holes with a suitable tube (a fragment homeomorphic to cylinder). The connected sum of two hypertopoids H3+ (Figure 34 C), using as a simplest tube the group CH2 or BH2- results in the dications (1) and (2). Both dications CH62+ (doubly protonated methane) and BH6+ (doubly protonated BH4- anion) are still unknown. However, the second pasting of a tube BH2- instead of other pair of hydrogen atoms (Figure 34 D) leads to the familiar diborane (3) with two (3c,2e) BHB bonds and one cycle (handle in the pseudomanifold). The third addition of BH2- anion to diborane (now as a homeomorphic insertion, labeling of bridging hydrogen atom) results in the known arachno-type anion B3H8-(4) with a BBB three-centered bond. Further 2D design of higher boron hydrides seems trivial, resembling the styx-description [111, 123].
New families of hypertopoids may be designed by pasting additional tubes to different spheres of the same hypertopoid H3+. The resulting families should differ in the number of handles, although within every family the homeomorphism should be manifested. Example of a long tube to be pasted is the (CH2)n chain that should appear instead of pair(s) of terminal hydrogen atoms. The addition of one, two, and three tubes is shown in Figure 34 E, F, G. The obtained structures (5), (6), (10), (11), (15), and (16) are well-known [109 -- 111]. These are famous families of nonclassical carbocations (like the norbornyl cation) either registered by spectral methods or unequivocally postulated as intermediates in carbocyclic and Meerwein-like rearrangements. (Most of the discussed cations with few exceptions, are short-living species for which it would be better to refer to as the intermediates.) Consider the homeomorphic shrinking of a chain to a single bond. This operation establishes homeomorphic relationship of three families of nonclassical carbocations to three cations: aromatic cyclopropenyl (17), delocalized allyl (12), and cation C2H5+ (7), that is, the protonated double bond of ethylene. This last step of shrinking is completely parallel to the homeomorphisms of larger cycles to the double bonds (although one edge is now a "hyperedge", that is, (3c,2e)-bond). However, the possibility of shrinking is still not exhausted.
The final step of homeomorphism in molecular pseudographs of localized structures was the topological shrinking of a multiple edge to a loop. This was "inessential" shrinking of the double bond in C2H4 to the lone pair in CH2 preserving the genus of a topoid. Now, the shrinking of a protonated double bond to the protonated lone pair may be also treated in terms of inessential homeomorphism of hypertopoids. Of course, the protonated ethylene (7) with (3c,2e) bond is an intermediate to form ethyl cation. Therefore, let us consider the protonated methylene (8) (with the formal (3c,2e) bond) also as an intermediate to form methyl cation. The difference is only that the "hyperedge" (that should be incident to 3 different vertices) is actually incident only to 2 vertices, although twice to one of them. Hence, it combines features of a loop and a normal edge resembling hyperloops in the pseudo-hypergraphs (see Section 2.2 and Figure 2).
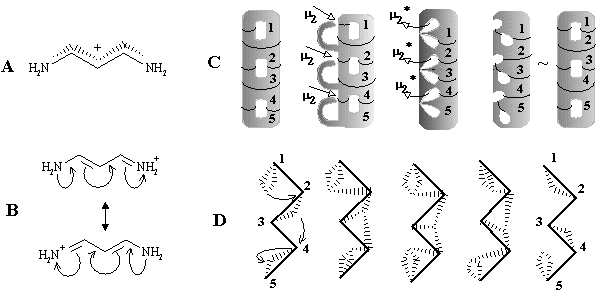
Such an assumption opens the possibility of visualizing the intermediate step of interaction between any Lewis acid and Lewis base centers. In particular, we may add one more Jordan curve to the hypertopoid of protonated methylene (8) and obtain the homeomorphic image (9), that is the intermediate for ammonia protonation related to the simplest hydrogen bond. Further additions of Jordan curves to the 2D image of structure (9) (insertion of CH2 or BH2-) symbolize intermediate states of bonding in BH3NH3 and quaternary ammonium salts CR3-NR3+. Now, we may shrink edges in the allyl and cyclopropenyl cations (12) and (17), making parallel to the interaction of a lone pair with carbocation in the immonium cation (14) and protonated cyanic acid (19). The diagrams of ethylene (13) and acetylene (18) (isoelectronic to the cations (14) and (19) and differed by the homological CH+ fragment from the cations (12) and (17)) may illustrate the intermediate step of heterolysis (polar resonance) of the multiple bonds.
The above homeomorphisms allow us to suggest how two lone pairs may be involved in multicentered bonding. Consider two cationic intermediates H3N+-H and H-NH3+ (each represented by formula (9) and hypertopoid in Figure 34 E) and make their connected sum (Figure 34 H) using the anion CH3- as a sort of a tube. The result is the delocalized cation (21), that is an intermediate for degenerated SN2 reactions. A homeomorphic shrinking of CH3- to H- (or, simply, homeomorphic removal of CH2) leads to the formula (20), the simplest example of hydrogen bond [NH3-H-NH3]+. The diagram (20) is also an intermediate step of the proton exchange between a conjugated acid (NH4+) and base (NH3). Shrinking of both terminal NH3 groups in the previous examples to H- results in the model systems [H-CH3-H]-(22) and [H-H-H]- (23) two "delocalized" lone pairs (cf. the topology of these anions H3- and CH5- with that of cations H3+ and CH5+).
One may conclude that the homeomorphism in topoids and hypertopoids has the same nature. In both cases the homeomorphism, that is, the preservation of the Euler characteristic, follows from the electron count. Therefore, the procedures of homological shrinking and expansion are heuristic tools in the establishing of novel similarity relationships for complicated cases of chemical bonding. In turn, a hyperloop may be recommended for use together with common styx-formulas.
11.4. Interconversion of Molecular Hypertopoids
Intuitively, any change of index mi of the base point requires a "touch" (that is, pasting) of 2D surfaces: otherwise, how would we make a bouquet without a touching? However, any such "touching" means either a decrease in the number of components or the appearance of a cycle (self-touching). Hence, the change of mi (and of the total M value) requires appropriate changes of the other invariants K, C, L for abstract pseudomanifolds.
The same is true for molecular topoids and hypertopoids. The bonds of various nature (two- or three-centered, one- or two-electron bonds) may be interconverted, and the processes may be described in terms of joining and disjoining of appropriate (pseudo)manifolds with changes in the values mi and M. The question is how the topological invariants K, C, L, M of molecular hypertopoids are interchanged in real reactions. In the preceding section, the invariance of c(W) within the homeomorphic series turns out useful to compare and classify the structures. We may suppose, that the principle of preservation of the Euler characteristic of hypertopoids in chemical reactions may be important to compare and classify the reactions. The assumption that Dc(W) = 0 immediately leads to (23):
(23) Dc(W) = 2DK -- 2DC -- DL + DM = 0,
which is the topological balance equation. If some parameters are not changed via a reaction, equation (23) is reduced. Thus, equations (12a) -- (12e) discussed in Section 7 for interchanges of the systems with localized bonds (M = 0), are still valid and meet the particular case DM = 0. For the cases where the index M is changed to other parameters (DM =/= 0) the following set of equations appears:
(24) DM = -- 2DK
(25) DM = 2DC
(26) DM = 2DC -- 2DK
(27) 2DK -- DL + DM = 0
(28) 2DC -- DL + DM = 0
(29) DM = DL
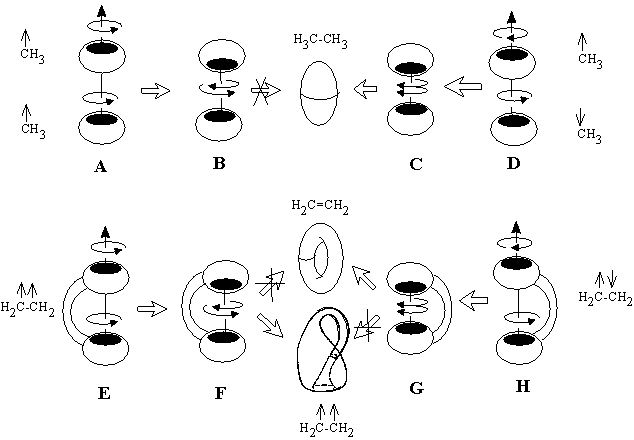
Let us retrieve the examples and inspect them with the goal to visualize the features of each interconversion (Figure 35).
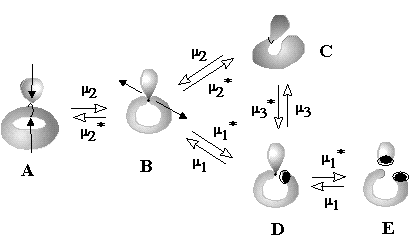
Heterolytic processes. First three equations (24) -- (26) correspond to polar processes (value L is preserved). Inspection of the right-hand parts of these equations shows that the change of index DM here is even, e.g., this may be a change from M = 0 to M = 2 or reverse. The simplest illustration of balance (24) is the change of a (2c,2e) bond (M = 0) to a (3c,2e) bond, like a protonation (or electrophilic alkylation) of a hydrogen molecule or alkane resulting in the series CnH2n+2+ (n may be zero).
The formation of the bouquet of three spheres W3(S0) from only two disjoint spheres is shown in Figure 35A. A sphere of an electron deficient species (H+ or CR3+) is moved closer to another sphere, that is the source of (2c,2e) bond. The localized bond represented as a Jordan loop (closed curve with a point) may be C-C, C-H or H-H bond. At the instant of touch the loop is "pinched" (as a sort of girdle tightening a sphere into two ones) and finally shrunk to a point to which three spheres become attached. Of course, the c value is preserved. Let us call the operation m2 (polar joining).
The formation of a (3c,2e)-bond is reversible (Figure 35A). Let us also reverse the operation m2 and disjoin the bouquet of spheres so that two usual spheres appear and call the operation m2* (polar disjoining). For instance, the hypertopoid H3+ may be disjoint to two spherical topoids H+ and H2. If the spheres would be labeled (say, by isotopes H, D, and T for the case H3+ or there may be different alkyl groups joint by the (3c,2e) bond) the disjoining m2* may occur in any of three directions. Indeed, the isotopic exchange (like H2 + D+ = H2D+ = HD + H+) and the interchange of alkyl groups in hypercarbon intermediates are well-known.
Topological operation m2 represents the first step of any polar interactions X + Y = Z, where X is an electron deficient species (Lewis acid) and Y is a Lewis base (real or masked) before the usual bond is formed. Hence, the formation of cationic intermediates (6) -- (9) (Figure 34) via the protonation of a cycle (in ammonia, carbene, ethylene, or cyclopropane) without destruction of the handle in a topoid is indistinguishable from the protonation of H2 and alkanes. These reactions belong to the same m2 type and follow the same balance equation (24).
The case corresponding to equation (25) appears if the connected sum of spheres is taken for the operation m2, say, if two complementary centers (Lewis base and acid) are at the ends of the same chain. Particular cases are the formation of the norbornyl cation, the processes of hydride migrations in alkyl cations, and resonance in allyl or cyclopropenyl cations. The reversed operation m2* corresponds to the "ring opening" of the protonated cyclopropane, ethylene, and ammonia (Figure 35B).
Equation (26) corresponds to the collapse of at least two components to a cycle with the appearance of multicentered bonds. Example is the dimerization reaction 2BH3 = B2H6 (Figure 35C).
Homolytic processes. The next three cases (27) -- (29) relate free electrons to multicentered bonding; here the changes in L (appearance or disappearance of holes) cause changes in M value. Evidently, these processes are important for structural modeling in the mass-spectrometry, where the bonding types are interchanged in ionized species.
The simplest case (27) is the gluing of a punctured sphere to a point on usual sphere making a bouquet; the topological change may be denoted as 1S + S0 = W2(S0). This may be formation of the radical cation H2+ from the radical H and cation H+ (or any homeomorphic case). Analogously, the radical addition to the (2c,1e) bond may cause formation of the (3c,2e) bond (Figure 35D). Let us call the operation m1 (homolytic joining) and consider the reversal operation m1* (homolytic disjoining), when a bouquet is destroyed so that any resulting surface may hang a puncture. Such homolytic disjoining is possible for the cation H3+, where the bouquet W3(S0) may be homolytically destroyed to another bouquet W2(S0) and a punctured sphere 1S0. The chemical image of the sequense m1 and m1* (shown in Figure 35D) may correspond to the isotopic exchange H2+ + D = H2D+ = HD+ + H.
Equation (28) appears for the case of "pinched torus" (an object obtained if a tube connects different spheres in the bouquet W2(S0)), and it helps to illustrate the cleavage of an ionized cycle to a chain (Figure 35E). The pinched torus of a cyclic radical cation after the cleavage m1* of the cyclic (2c,1e) bond is destroyed to a stretched punctured sphere, and the appeared free radical and cationic centers are on the opposite ends of the chain.
The last equation (29) is essential. Expression DM = DL is the case when everything else (namely, C and K) is fixed. Then, one puncture (free electron) may appear only if it is compensated by the increase of M by one. This may be possible for an intermediate step of conversion of the "non bonding" free radical center to a bond; let us denote this operation m3. The reverse process (operation m3*) may be an intermediate step of homolysis of a bond. We can not refer to the operations m3 and m3* as polar or radical, they are independent on the type of formed or broken bond. Rather, these processes should be related to the topological change of a molecule via a photochemical excitation and mass-spectral rearrangement. If an electron leaves the region of the usual bond (single or multiple) with mi = 0, the residual domain should acquire the properties of a (2c,1e)-bond with mi = 1 (Figure 35F). Analogously, a puncture may "appear" from the region of a (2c,1e) bond (mi = 1), and the remaining region should acquire the properties of the base point with mi = 2, i.e., the novel (3c,2e) bond should appear. Finally, we may consider an analogous shift of a puncture from the area of the (3c,2e) bond, that requires a decrease of M (or mi) from 2 to 3. This is possible for W4(S0), bouquet of four spheres. Therefore, one may imagine a weak (3c, 1e) bond (for instance, in the hypothetical dication H32+) as the bouquet W4(S0).