Eugene Babaev "Intuitive Chemical Topology Concepts" (c)4. Intuitive Chemical Concepts Related to Topology
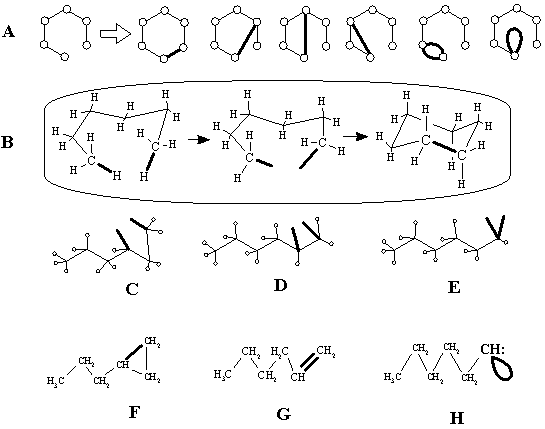
Intuitive cut-and-paste. Consider the relation between a chain and a cycle, e.g., between n-hexane C6H14, which does not have cycles, and the closest family of monocyclic isomers C6H12 having a cycle with three to six carbon atoms. A chain in an abstract graph (drawn on paper) is easily converted to a cycle by simply adding a new edge somewhere in a tree (Figure 12A). However, it is impossible to create the molecular graph of cyclohexane by adding a new edge to the molecular graph of hexane. This would violate vertices’ degrees, which are constant according to the context of our consideration. Instead, it is necessary to remove two hydrogen atoms first, and then join the emerging "free valencies" to a cycle (Figure 12B). Free valences have direct experimental evidence [86]: these are free radical centers.
The closure of a cycle by stepwise removal of hydrogen atoms and formation of a bond is an intuitive topological process. The operation resembles cut-and-paste procedure in the topology of surfaces. The removal of two hydrogen atoms is cutting (making two holes), and formation of the C–C bond is gluing the holes. Generally, the choice of the pairs of hydrogen atoms to be cut from the n-hexane chain may be random, and the mental pasting should, indeed, result in 5-, 4-, and 3-membered cycles, all isomeric to cyclohexane. An example of such "cut-and-paste" from hexane C6H14 to propylcyclopropane C6H12 is shown in Figure 12C, F.
Figure 12. (A) Conversion of a chain into a cycle in an abstract graph by drawing a new edge. (B) The same process shown as a "cut-and-paste" operation in molecular graphs; free valencies are shown in bold. (C), (D), (E) Random choice of two hydrogen atoms for cut in the structure of hexane. A monocyclic molecular graph (F), a multigraph (G), and a pseudograph (H) (represented by common structures) obtained after pasting of free valencies in diagrams (C), (D), and (E).
One may easily imagine the cut of two hydrogen atoms adjacent to a neighboring carbon atoms (as in Figure 12D). In this case the mental cut-and-paste results in the formation of a double bond, familiar to chemists [87], and the structures are isomeric hexenes C6H12 (e.g., Figure 12G). Finally, the pair of removed hydrogen atoms may even be incident to the same atom (Figure 12H). Here, the mental cut-and-paste should result in the appearance of an edge incident to the same vertex, that is, in a loop (Figure 12D). Although this situation is less trivial, such a class exists and is familiar to an organic chemist. These are carbenes [88] where the "free valencies" are joined together into a lone pair. Random cut-and-paste in n-hexane molecule results in three isomeric carbenes of the C6H12 formula.
The mental picture discussed above is related to the intuitive chemical topology: a double bond and a loop of carbenes (the lone pair) are intuitively indistinguishable from larger cycles, at least in their origin (cf. all diagrams in Figure 12). However, the concepts of a lone pair and a multiple bond are in conflict with physical models. Furthermore, although a lone pair is an important chemical concept used for decades, it is still ill-defined even in terms of graphs or surfaces. The same is true for the modeling of free radicals. The situation appears somewhat paradoxical: lone pairs, free radicals, and multiple bonds are responsible for essential changes in molecular topology (like interconversions of chains to cycles and disconnected sets to connected ones), and chemists yet have a poor idea of how to express them in graphs or surfaces. Let us overview some aspects.
Double bond. The concept of multiple bonds (double or triple) appeared during the last century. The goal of this concept was to preserve the valence of a carbon atom in an unsaturated compound, and now the multiple bond notation is beyond any question in the chemical literature [87]. The multiple edge naturally falls into the definition of a molecular multigraph with a "two-membered" cycle, because its appearance (as the appearance of any larger cycle) increases the cyclomatic number of a multigraph by one, and the subsequent removal of a double bond (like the destruction of a cycle) produces a tree. In early ball-and-stick models, the double bond was presented by two bent cylindrical tubes, and the 2D surface of such a solid 3D model is, of course, homeomorphic to a torus. The intuitive argument, approving these models of the double bond, is clearly related to the homeomorphism concept. If any member of the family of cycloalkanes CnH2n (no matter the size of a cycle) matches topology of the torus (x = c = 0), then it is natural to consider C2H4 (n = 2) as being a specific case within this series.
In the space-filling and VDW models, the atoms forming a bond are considered to be spherical domains. Here, the model of a cyclic molecule CnH2n has a toroidal surface formed by overlapping spheres; even three spheres may be adjacent in such a way to leave a hole. However, in the case of double bond, it is impossible to imagine a hole between two adjacent spheres; the multiple contact A=B is reduced to a single contact. Therefore, the decrease in the cycle size (say, from 3 to 2) within the series CnH2n results in the shift of the toroidal feature to the spherical one, in contrast to the homeomorphic shrinking of a large cycle to a bent bond in the ball-and-stick models. Such a pronounced conflict in the topology of two traditional models of a double bond is a serious problem in chemical education. The author remember a handbook for secondary school students that recommended: "to make a double bond, one should take a solid ball and put two matches (or sticks) inside". Also, in some modern computer programs the choice of the "ball-and-stick" option in the menu results only in one stick for C=C bond.
The elegant idea of the "banana-like" double bond [89, 90] in the valence bond theory [91] perfectly matches the classical bent bonds. Also, in MO theory the principle of localized orbitals may be used to visualize double bond in somewhat similar manner [85]. Two pairs of localized orbitals doubly overlap resembling a bent multiple bond. However, this does not mean that the toroidal feature of a bond is reflected in molecular orbitals. First, orbitals have nodes at atoms. Second, the equivalent picture of a C=C bond (one s- and one p-bond) corresponds to at least triple overlap of p-orbitals in different regions (one contact in the plane of a C2H4 molecule and two contacts higher and lower the plane), as if it would be the topology of a pretzel.
The concept of bent "banana-bond" contradicts some other physical models. Thus, the isodensity contour surface for ethylene provides no evidence for the expected "emptiness" between bent bonds (which is observed for larger cycles). On the contrary, there is an excessive charge density for the double bonds. Also, there is no appropriate "cycle-like" critical point for the C=C bond in the gradient of the electron density Ñr(r), and the Figure 10F (just the case of ethylene) displays the absence of a feature that may resemble larger cycles. Therefore, the extracted bipartite graph of an alkene CnH2n in the Bader’s model [71--73] is a tree rather than a multigraph. As a compensation, the concept of ellipticity of bonds is used to describe the difference between single and multiple bonds. Hence, the supply of topological objects in physical models of a double bond is diverse (sphere, torus, pretzel, etc.), and the models themselves are frequently revisited.
Free radicals and open-shell molecules. The thermal or photochemical decomposition of saturated hydrocarbons results in highly reactive short-living species, free radicals [86]. Although the precursors have well-defined molecular graphs and 2D surfaces, the products have not. Radicals have unpaired electrons, and there may be several unpaired electrons as in a biradical molecule (like O2). It is still unclear how to combine these "free valences" with the molecular graph concept. In the Lewis dot formulas [92, 93], the radical center is a single dot near an atomic symbol. In the Linnet double-quartet theory [94], an odd number of dots may appear between a pair of atoms. Because free electron has a spin, an oriented arrow is frequently assigned to the free radical center to indicate direction (the sign) of the spin. In triplet states, the arrows are collinear (Hund’s rule), whereas the recombination of free radicals requires opposite (antiparallel) spins. Drawing of energy levels (with directed arrows) frequently substitutes drawing the structures of radicals. In physical models of radicals, the concept of spin density distribution is used. Although it is possible to draw an isodensity 2D surface of such a 3D body, it is unclear how a graph-like object can be reconstructed from it.
The above-mentioned mental pasting of "free valencies" (Figure 12) corresponds to a real process. Two disjoint radicals may recombine to a connected molecule, and a single biradical may actually (not only imaginary) recombine forming a molecule with a cycle, a double bond, or a lone pair. The processes are treated as the conversion of excited triplet states of molecules to the singlet states. Thus, trimethylene biradical forms cyclopropane, triplet ethylene is converted to the "usual" ethylene (having a double bond), and triplet methylene is changed to singlet methylene with a lone pair.
Lone pairs and vacancies. A lone pair is another example of a concept which carries much information for a chemist, but has no exact physical meaning. This concept has been first introduced by Lewis and formed the basis for later electronic theories of chemical bonding. Lone pairs are used to describe the formation of donor–acceptor bonds; another application of lone pairs is prediction of molecular geometry. Traditional representation of a lone pair by Lewis and Langmuir [93, 95] involved a pair of dotes located near an atom symbol, although from the topological viewpoint, this is a rather poor image. There is still no general convention how lone pairs may be expressed in classical 2D models, therefore their presence is always ignored. Only in the Gillespie–Nyholm approach to molecular geometry [96 -- 98] is the lone pair (a nonbonding domain) considered as an object equivalent to a bonding domain with respect to arrangement of both domain types around an atom. In the pictorial form this arrangement is expressed as a cluster of touching 3D spheres or even as a set of 1D circles on a 2D sphere.
In physical models some excess of the electron density function (and some convex domains in contour surfaces) may be assigned to lone pairs. In the Bader model, lone pairs appear as definitive critical points in the Laplacian of charge density Ñ2r, but not in the Ñr analysis (that allows one to extract a graph) [73]. Nevertheless, it may be visualized at least as 2D image, either in the perspective drawing of a contour map [73], or as 2D isosurfaces in R3 (see an excellent pictorial presentation on WWW pages [99, 100]). Hence, it is still an open question how to "extract" the lone pair to molecular graphs. Furthermore, there is no physical evidence for the existence of a lone pair, since there are no reasons why two electrons should occupy the same region.
The concept of a lone pair plays a fundamental role in the description of heterolytic cleavage and formation of chemical bonds, as reflected in the concept of Lewis acids and bases [101]. A Lewis base (e.g., NH3) has a lone pair, and a Lewis acid (e.g., BH3) has a vacancy (the lack of electron pairs to form the stable octet configuration of a noble gas). The vacancy thus defined is also hardly representable in molecular graphs or surfaces, although it is related to depletion of the charge density. Sharing of a lone pair (donated from the base to the acid) results in the formation of a donor–acceptor (coordination) bond (BH3 + NH3 = NH3BH3). Reactions of this sort, which are familiar even to undergraduates, incorporate the same logical "modeling paradox" as do the recombination of two free radicals: a molecule with a well-defined graph and well-defined 2D surface is formed from ill-defined model structures.
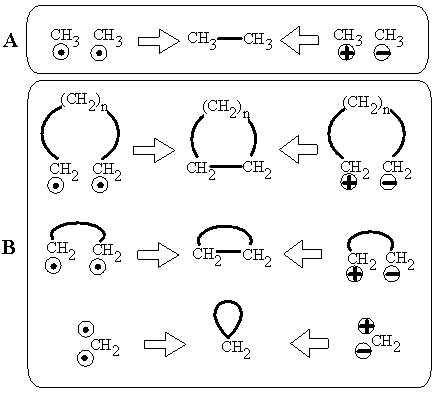
The center of Lewis acidity or basicity may be located in the carbon skeleton with localized bonds. Examples are carbanions (CH3– with a lone pair) and carbocations (CH3+ with a vacancy). In molecular graphs, these centers may be visualized considering the sign of a charge as a vertex label. Complementary centers may recombine to an ordinary covalent C–C bond (e.g., CH3+ + CH3– = CH3–CH3) resembling recombination of radicals (Figure 13A).
Let us proceed from this analogy and consider the formation of a cycle (Figure 13B). A long chain between dual centers (a zwitter-ion) may be closed to a large cycle. The shortest chain (i.e., bond) between cation and anion (CH2+–CH2–) may also be "closed" to a small cycle, that is the double bond CH2=CH2. (Indeed, this zwitter-ion is known as a polar resonance form of a double bond.) Therefore, a double bond appears in the same manner as any other cycle from an acyclic zwitter-ion. Finally, there is intriguing possibility to place the dual centers (cationic and anionic) as close as possible, to the single atom. Such coalescence of CH3+ and CH3– in the single carbon atom is the case of methylene CH2 (in the singlet state), which is not charged. Methylene is the ambivalent species, having both a lone pair and a vacancy and acting as both a Lewis acid and a base.
Figure 13. (A) Two possibilities to obtain a molecule with a well-defined molecular graph from two molecules (with ill-defined molecular graphs), either from radicals (left) or from ions (right). In both cases a disconnected set is recombined to a connected molecule. (B) Intuitive topological equivalence of a large cycle, double bond, and lone pair (middle column) in respect to formation of a cycle from biradicals (left column) or dipolar chain (right column). Radical centers are labeled by dots.
Hence, "obtaining" the lone pair of methylene from either a biradical or by coalescence of dual centers confirms its direct relation to the large cycle and to the double bond. In addition, let us remember that CH2 is the smallest possible homologue of the CnH2n family (n = 1), which has the unit cyclomatic number for any member. The analogy of the lone pair to a loop (as a smallest cycle in a graph) and to the topology of torus (x = c = 0) is pronounced, although this is a somewhat strange image: an extremely bent bond that connects an atom to itself. The model is not completely new. Rather, it is century-old. It was suggested by Nef in 1896 for CH2 in his "methylene theory" [102].
The examples discussed above illustrate deep relationships between fundamental chemical concepts, surface topology, and homeomorphism. However, these concepts, especially lone pairs and free radicals, are still ill-defined in terms of common graphs and 2D models. It seems that accurate mathematical redefinition of these concepts may lead to a picture, which is self-consistent at least chemically. Why not use the homeomorphism concept to approach better harmony in commonly used classical models? Let us explore this possibility.
5. Topology of a Lewis Formula: Pseudograph, Graphoid, and Topoid
5.1. Molecular Pseudograph
The apparently clear term molecular graph, discussed in Section 3.1, is actually ill-defined: chemists commonly use various sorts of molecular graphs [1, 3, 9]. For instance, it is frequently useful to assign vertices and edges of a graph only to some "important" atoms and/or bonds. One may consider only "heavy" atoms (as in the so-called hydrogen-suppressed graphs) or the bonds representing only s-frameworks (graphs for p-systems). A single vertex may also represent a functional group. These graphs (and even molecular multigraphs with multiple edges) are "incomplete" in the sense of original Lewis dot formula that consists of all atoms and all valence electrons (represented by dots). Perhaps, the best image of a Lewis formula is the molecular pseudograph, a multigraph with loops representing lone pairs. Only this graph represents all valence electron pairs by edges (including nonbonding lone pairs) and all atoms. As we mentioned, Nef pioneered the use of loops 20 years before Lewis’ suggestion of pairs of dots, and this intuitive graph-theoretical idea was overlooked.
A clear model of molecular pseudographs appeared only in 1970s after the papers of Ugi et al. [103, 104]. Ugi used the representation of a molecule by a connection table (BE-matrix) that resembles adjacency matrices for multigraphs but with number of valence electrons for each atom (zi) on the main diagonal. (For atoms from Main groups of the Periodic system zi<8.) The loop appears automatically when reconstructing a graph from the matrix, because entries of the main diagonal denote the numbers of valence electrons, necessary for correct count of vertex degrees in a molecular pseudograph. Sometimes, molecular pseudographs appeared in different fields of mathematical chemistry (e.g., [32, 105, 106]). However, they are rarely used. Probably one of the reasons is that chemists frequently draw "lobes" of p-orbitals near the atoms in molecular graphs, and the loops may be confused with p-orbitals. Because nobody has popularized the model, let us discuss whether a pseudograph has any advantages.
(i) Cycles and electron count. Equations (1) to (3) are equally valid for an ordinary graph or a pseudograph. Because vertex degree in molecular pseudograph is deg vi = zi, we may write S deg vi = E = S zi = Z/2 and transform the equations (1)--(3) to equation (8a) for molecular pseudographs. Above, we used equation (8a) to count ordinary cycles in the hydrocarbons from balance of N and Z. Therefore, a lone pair and a double bond belong to the same sort of cycles, as does any large cycle, not because of arbitrary definition, but because of the correct electron count.
(ii) Invariance of valency. The value deg vi is a local property of a point, indicating how many e1 elements appear in the neighborhood of a point e0. If deg vi is fixed, then it is unimportant for a point what happens to the second "end" of an incident edge: this "end" may be closed to a loop, attached to an incident vertex, or to several vertices. Because an atom contributes to a molecule fixed value zi and zi = deg vi, the value zi should also be locally constant and independent of any environment around an atom. For instance, the neutral carbon atom may be oxidized, reduced, have any number of neighbors of any nature, and the terms "oxidation state", "coordination number", and "valence" may not coincide in the series like CO2, CO, CH4, and CH2. Nevertheless, the vertex degree of every pseudograph is locally preserved, because equation deg vi = zi = 4 means that a carbon atom belongs to the 4th main group in the Periodic Table of Elements. Recall that in pseudographs of CO and CH2, a loop formally adds two valencies to a vertex.) For a nitrogen atom, deg vi = 5 should be assigned in either of these cases: HNO3, HNO2, NH2OH, or NH3. This property is unique for the molecular pseudograph [31, 32] and is violated in any other "molecular graphs" with heteroatoms as labels.
(iii) Isomorphism and similarity. The number of valence electrons zi is not the charge of a nucleus of element, and value zi may be the same for isovalent atom(s) and ion(s). The same is true for the vertex degree. Therefore, unique pseudograph may represent several isovalent species, that have the same Lewis dot formulas (cf. series CH4, NH4+, BH4-, and BeH42– or NO3–, CO32–, and BO32–). More explicitly, within such series the molecules have isomorphic pseudographs. This is convenient, because the isoelectronic series are usually isostructural [29, 95, 107, 108], and therefore, the geometrical similarity may be expressed in terms of isomorphism of molecular graphs. Thus, isomorphic pseudographs of isoelectronic series NH3, PH3, and CH3– (with total of 4 edges and the pyramidal shape) are not isomorphic to pseudographs of another isoelectronic series BH3, AlH3, and CH3+ (with total of 3 edges and the planar configuration). This helps one to avoid uncertainties like drawing the same graph to apparently isostructural BH3 and NH3 (which, in fact, are not), as in many graph-theoretical approaches and computer software.
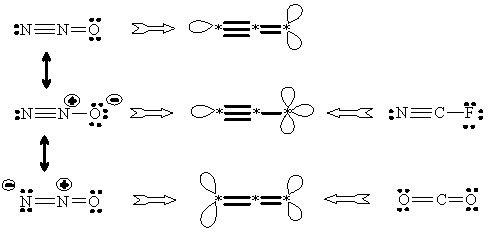
(iv) Octet rule and resonance. Old, but still useful, octet rule [95] is translated as the preference of four edges incident to a vertex. Of course, a loop is only one edge (although with two ends). In pseudograph of NH3, despite local deg vi is 5, there are only four edges (of which one is a loop) and the octet configuration is valid. For the case where the structure violates the octet rule (like HNO3 or N2O) the charges may be redistributed until the octet structure is achieved. This procedure causes a transformation of a graph to another one. In terms of pseudographs, a set of nonisomorphic graphs (resonance forms) is assigned to the same molecule (see Figure 14). On the other hand, different molecules may have the same (isomorphic) pseudograph (cf. zwitter-ion NH3BH3 with the covalent structure CH3CH3 and other examples in Figure 14).
Figure 14. Relationship between resonance structures expressed by means of isomorphism of pseudographs. On the left: design of resonance structures for N2O to obtain the octet configuration. In the middle: pseudographs corresponding to the resonance structures. On the right: octet molecules with pseudographs isomorphic to pseudographs of resonance structures.
We may conclude that some chemical terms and concepts (that may have imprecise definition in classical molecular models) become clearer after being translated into the language of pseudographs, because the pseudographs seem to coincide with Lewis formulas. Furthermore, every abstract pseudograph corresponds (if at all) to only a finite set of specific molecular pseudographs (see previous paragraphs).
It is clear why a tree (Figure 10F) cannot represent chemical structure of ethylene. Topology of a tree contradicts to equation (8a) and chemical formula C2H4. The place for this tree (with deg vi = 3 and deg vi = 1) is not vacant; such a graph may be isomorphic to H2B–BH2, H2B–CH2+, at least to the dication of ethylene, but not to the ethylene with value C = 1 deduced from electron count. Therefore, bipartite graphs extracted from Ñr(r) analysis, only in partial cases (namely, for saturated hydrocarbons) are isomorphic to chemical graphs. The intrinsic topology of Lewis formulas is different from the topology of critical points, and it is still not clarified in the mathematical sense.