Вариант 13

1. Молекулярная сумма по состояниям, связанная с электронными состояниями, равна:

q_el = g₀ + g₁ exp(- /kT),

где g₀, g₁ - кратности вырождения основного и первого возбужденного электронных уровней. Следовательно,

q_el = 2 + 4^. exp(-/kT),

и мольный вклад электронных движений в изохорную теплоемкость равен:

C_V,el = 2RT( lnq_el / T)_V + RT( ² ln q_el / T²)_V =

= R (/kT)² (g₁/g₀) exp(/kT) [exp(/kT) + (g₁/g₀)]^-2 =

= 2R (e /kT)² exp(e /kT) [exp(e /kT) + 2]^-2 =

= 2^. 8.314^. (0.573)^2. 1.774 / (1.774 + 2)² = 0.68 Дж/моль^. К.

C_V,rot = 2RT ( lnq_rot / T)_V + RT² ( ²lnq_rot / T²)_V = R.

C_V = 8.31 + 0.68 = 9.0 Дж/моль^. K..

2.

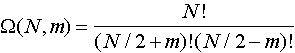
При N >> 1 применяя формулу Стирлинга: lnN! = NlnN - N + 1/2ln(2N), получаем:

ln(N,m) = lnN! - ln(N/2 + m)! - ln(N/2 - m)! =

= NlnN - (N/2 + m)ln(N/2) - (N/2 + m)ln(1 + 2m/N) - (N/2 - m)ln(N/2) -

- (N/2 - m)ln(1 - 2m/N) + 1/2ln(2/N) - 1/2ln(1 + 2m/N) - 1/2ln(1 - 2m/N).

Полагая далее 1 << m << N, и преобразуя логарифмы с точностью до линейных членов, получаем:

ln(N,m) = ln(N,0) - 2m²/N, или (N,m) =(N,0) exp(-2m²/N),

где (N,0) = 2^N(2/N)^1/2 - наиболее вероятное число состояний системы, отвечающее значению m = 0.

Поскольку величина M = 2m представляет собой суммарный магнитный момент системы, последнее соотношение можно записать в виде:

(N,M) =(N,0) exp(-M²/2N).

Найденная функция распределения удовлетворяет условию:

(N,m) = (N,m) dm = 2^N,

поскольку 2^N есть полное число состояний системы.

3.

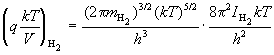
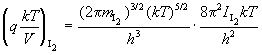
кДж/моль.

 
=
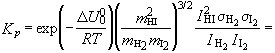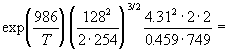