Теоретические задачи

Задачи 1-5

Задача 1. Вода
Задача 2. Газы Ван-дер-Ваальса
Задача 3. Скорости и механизмы реакций
Задача 4. Ферментативный катализ
Задача 5. Уравнение Шредингера

Задача 1. Вода
Вода - самое распространенное вещество в окружающей среде - прекрасная система для демонстрации многих понятий термодинамики. Она может существует в трех фазах: твердой (лед), жидкой и газообразной. [При высоких давлениях существует несколько различных модификаций льда, но это выходит за рамки задачи]. Фазовая диаграмма воды, которая описывает зависимость равновесного давления от температуры для различных фаз, имеет вид:

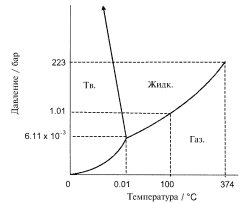
А. Фазовая диаграмма

Фазовая диаграмма воды (без масштаба)

а. При каких температуре и давлении все три фазы воды находятся в равновесии?
б. По диаграмме определите, как влияет понижение давления на температуру кипения воды и температуру плавления льда.
в. Кривая равновесия "жидкость-пар" заканчивается в точке P_c = 223 бар и T_c = 374 ^оС. Что означает эта точка?
г. Какая фаза воды устойчива при T = 300 K, P = 12.0 бар; T = 270 K, P = 1.00 бар?
д. Ниже какого давления лед при изобарном нагревании будет сублимироваться в пар?
е. При некоторых температуре и давлении на кривой "жидкость-пар" молярные объемы воды в двух фазах равны:
м³ м³.
Рассчитайте объемные доли воды жидкости и пара в сосуде объемом 0.100 л, содержащем 1.00 моль воды.

Б. Уравнение Клаузиуса-Клапейрона

а. Объясните ответ на вопрос А, б с помощью уравнения Клапейрона.
б. В автоклавах, используемых в медицине для стерилизации, вода должна кипеть при температуре 120 ^оС для того, чтобы убить большую часть бактерий. Оцените необходимое для этого давление. Мольная энтальпия испарения воды равна 40.66 кДж^. моль^-1 в нормальной точке кипения. Укажите, какие допущения вы использовали при оценке.
в. Мольная энтальпия плавления воды в нормальной точке замерзания (273.15 K) равна 6008 кДж^. моль^-1. Оцените давление, при котором вода и лед находятся в равновесии при температуре -0.200 ^оС. Плотность льда = 917 кг^. м^-3, плотность воды = 1000 кг^{. .} м^-3. Укажите, какие допущения вы использовали при оценке.

а. Возьмем 28.5 г переохлажденной (жидкой) воды при -12 ^оС и 1.00 бар. Находится ли это состояние в плоскости P - T на фазовой диаграмме?
б. Это метастабильное состояние внезапно переходит в лед при этих же температуре и давлении. Считая метастабильное состояние равновесным, рассчитайте, сколько теплоты выделится при этом. Мольные теплоемкости, которые можно считать постоянными, равны:
Дж^. моль^-1. К^-1

Дж^. моль^-1. К^-1

Дж^. г^-1

в. Определите общее изменение энтропии Вселенной в результате этого процесса и покажите, что этот результат подтверждает Второй Закон термодинамики. Температуру окружающей среды примите равной -12 ^оС.

Из уравнения состояния идеального газа PV = nRT следует, что фактор сжимаемости равен 1:

Однако, для реальных газов фактор сжимаемости отклоняется от 1. Для того, чтобы описать поведение реальных газов, Ван-дер-Ваальс предложил следующее уравнение состояния:

,

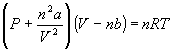где a и b - индивидуальные постоянные для газа. Постоянная a служит мерой межмолекулярного взаимодействия, а постоянная b связана с собственным размером молекул.

а. Используя уравнение Ван-дер-Ваальса, покажите, что:

1. При достаточно высоких температурах Z больше единицы при всех давлениях. При высоких температурах и низких давлениях Z стремится к значению идеального газа.
2. При низких температурах Z может быть меньше единицы.
3. При a = 0, Z линейно растет с ростом давления.

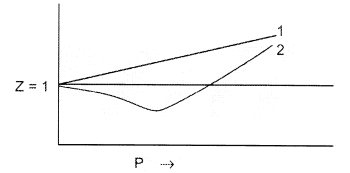
б. На рисунке приведена зависимость Z от P при некоторой температуре для He и N₂.

Для He, a = 3.46 10^-2 бар^. л^2. моль^-2, b = 2.38 10^-2 л^. моль^-1.
Для N₂, a = 1.37 бар^. л^2. моль^-2, b = 3.87 10^-2 л^. моль^-1.
Укажите, какой график соответствует He, а какой - N₂.

в. На рисунке приведены две P-V изотермы газа Ван-дер-Ваальса. Укажите, какая из них соответствует температуре ниже критической (T_c) для данного газа.

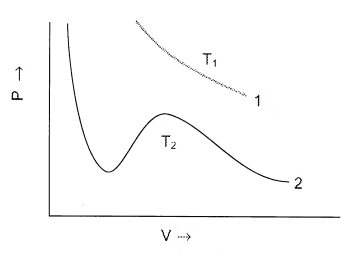
г. Для заданного P, три корня уравнения Ван-дер-Ваальса сливаются при некоторой температуре T = T_c. Выразите T_c через a и b и, используя этот результат, покажите, что N₂ сжижается легче, чем He.
д. Определите работу, совершаемую одним молем газообразного N₂ при обратимом изотермическом расширении от 1.00 л до 10.0 л. Примите, что N₂ описывается уравнением Ван-дер-Ваальса.

Одно и то же кинетическое уравнение для химической реакции может соответствовать нескольким разным механизмам. Для реакции

H₂ + I₂ 2HI
экспериментальное кинетическое уравнение имеет вид:

В течение долгого времени полагали, что реакция протекает так, как написано в уравнении, т.е., что она представляется собой элементарную бимолекулярную реакцию. В настоящее время считают, что реакция может протекать по нескольким механизмам. Ниже определенной температуры предложены два альтернативных механизма:
(1) I₂   2I (константа равновесия K)

	k1
I + I + H2		2HI

(2) I₂   (I₂)_d (константа равновесия K')

	k2
(I2)d + H2		2HI

   где (I₂)_d представляет распадное (несвязанное) состояние I₂. В каждом механизме первая стадия - быстрая, а вторая - медленная.

а. Покажите, что оба механизма соответствуют экспериментальному кинетическому уравнению.
б. В таблице приведены значения константы скорости реакции k при двух температурах:

1. Определите энергию активации E_a.
2. Энергия связи в молекуле I₂ равна 151 кДж^. моль^-1. Объясните, почему вторая стадия в каждом механизме является лимитирующей.

в. Изменение внутренней энергии ( U) в суммарной реакции равно -8.2 кДж^. моль^-1. Определите энергию активации обратной реакции.
г. Энергия активации реакции бывает отрицательной. Пример - рекомбинация атомов иода в газовой фазе в присутствии аргона: I + I + Ar I₂ + Ar, для которой энергия активации примерно равна -6 кДж^. моль^-1.
Один из возможных механизмов этой реакции: I + Ar + Ar IAr + Ar (константа равновесия K'')

	k3
IAr + I		I2 + Ar

   где IAr - очень слабо связанная молекула.

1. Предполагая, что вторая стадия - лимитирующая, выведите кинетическое уравнение для этой реакции.
2.Объясните, почему энергия активации для рекомбинации иода - отрицательная.

Ферменты играют ключевую роль во многих химических реакциях в живых организмах. Некоторые ферментативные реакции можно описать простым механизмом Михаэлиса-Ментен:

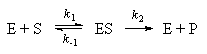
где E обозначает фермент, S - субстрат, на который действует фермент, а P - конечный продукт реакции.

Предположим, что вторая стадия необратима, а равновесие на первой стадии устанавливается очень быстро.
а.В эксперименте начальную скорость (образования P) определяли при различных концентрациях субстрата, поддерживая общую концентрацию фермента постоянной и равной 1.5 10^-9 М. При этом получили следующую зависимость:

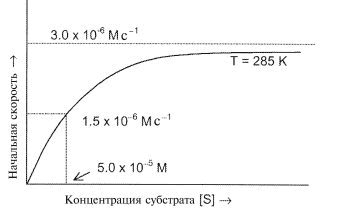
1. При малых [S] зависимость - линейная, а при больших [S] она стремится к постоянному значению. Покажите, что эти свойства соответствуют механизму Михаэлиса-Ментен. (Используйте приближение стационарных концентраций для промежуточного комплекса).
2. Определите константу скорости k₂ для второй стадии.
3. На базе механизма Михаэлиса-Ментен предскажите начальную скорость реакции при концентрации субстрата [S] = 1.0 10^-4 М.
4. Определите константу равновесия образования фермент-субстратного комплекса ES.

б. Описанный эксперимент, который был проведен при 285 К, повторили при другой температуре (310 К) с той же самой общей концентрацией фермента, и получили аналогичную кривую:

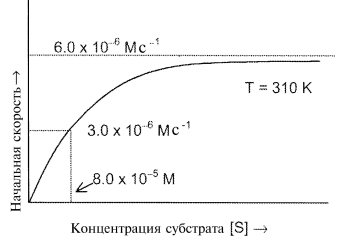
Определите энергию активации превращения ES в E и P

в. Интересное приложение ферментативного катализа состоит в том, что ферменты инактивируют антибиотики. Так, антибиотик пенициллин инактивируется ферментом пенициллиназой, выделяемым некоторыми бактериями. Этот фермент имеет один активный центр. Предположим для простоты, что данная реакция описывается константами скорости, определенными выше в п. а. Допустим также, что доза 3 мкмоль антибиотика вызывает выделение 2.0 10^-6 мкмоль фермента в 1.00 мл бактериальной суспензии.

1. Определите долю фермента, которая связывается с субстратом (пенициллином) на начальной стадии реакции.
2. Определите время, необходимое для инактивации 50% дозы антибиотика.

г. Предположим, что для управления инактивацией пенициллина введено вещество, которое имеет похожую на пенициллин структуру и может занимать активный центр фермента, однако не обладает биологической активностью. Это приводит к ингибированию ферментативной реакции. Степень ингибирования определяется следующим образом:
, где r и r₀ - начальные скорости ингибируемой и неингибируемой реакции, соответственно.
Рассмотрим следующий механизм ингибирования:

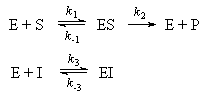
1. Покажите, что степень ингибирования понижается с увеличением концентрации субстрата (при постоянной концентрации ингибитора), и ингибитор становится неэффективным при больших концентрациях субстрата. (Такая механизм ингибирования называется конкурентным).
2. При низкой концентрации субстрата пенициллина определите, какая концентрация ингибитора вызовет понижение скорости инактивации пенициллина в 4 раза. Константа диссоциации комплекса "фермент-ингибитор" равна 5.0 10^-5.

Простейшее уравнение Шредингера, описывающее частицу, которая свободно движется в одномерном "жестком" ящике, имеет фундаментальное свойство: граничные условия для волновой функции приводят к квантованию некоторых величин.
а. Электрон массой m движется по оси x и заперт между точками с координатами x = 0 и x = L. Во всей этой области движение электрона - свободное, на него не действуют никакие силы.

1. Напишите стационарное уравнение Шредингера для волновой функции электрона y .
2. Какие из перечисленных функций могут быть волновой функцией электрона в одномерном жестком ящике:
1)
2)
3)
4) ,где k - любое действительное число, а n - натуральное число?
3.Покажите, что волновым функциям из вопроса а.2 соответствует энергия

4. Изобразите графики волновых функций электрона в основном и в первых двух возбужденных состояниях. Какое число узлов (в области между x = 0 и x = L) имеет волновая функция с энергией E_n?
5.Нормируйте волновую функцию основного состояния электрона. (Интеграл от квадрата модуля нормированной волновой функции по всему пространству должен быть равен единице.)

б. Интересным примером использования этой одномерной модели в химии служит описание движения электрона по сопряженной системе одинарных и двойных связей. Молекула бутадиена-1,3 имеет 4 -электрона, которые, согласно этой модели, свободно двигаются по линии, включающей три углерод-углеродные связи примерно одинаковой длины (1.4 10^-10 м) с добавлением отрезка 1.4 10^-10 м на каждом краю. Используя принцип наименьшей энергии, изобразите схему заполнения электронами энергетических уровней. Рассчитайте наименьшую энергию возбуждения системы.

в. Граничные условия для волновой функции приводят к квантованию не только энергии, но и других физических величин, таких как момент импульса. Волновая функция, соответствующая значению z-компоненты момента импульса L_z = h /2 , имеет вид:
,
где f - (азимутальный) угол, описывающий положение в плоскости x-y относительно оси x. Покажите, что условие однозначности этой функции в каждой точке пространства приводит к квантованию . Определите квантованные значения проекции момента импульса на ось z.