Читателю предлагается первая книга трехтомного издания, посвященного задачам
Международных Менделеевских олимпиад школьников по химии. В настоящий том
включены задания теоретических задач, решения которых можно найти во втором
томе трехтомника. Третий том серии посвящен заданиям экспериментальных туров.
Публикуемые задачи - результат работы большого коллектива авторов (их имена
приведены перед решениями каждой задачи). Уникальный материал, представленный
в книге, будет полезен всем, кто интересуется химией: школьникам, студентам, учителям школ и преподавателям вузов.
Содержание
| Предисловие |
|
4 |
| XXXVI МЕНДЕЛЕЕВСКАЯ ОЛИМПИАДА 2002 г. |
|
10 |
| I ТЕОРЕТИЧЕСКИЙ ТУР |
|
10 |
| II ТЕОРЕТИЧЕСКИЙ ТУР |
|
13 |
| XXXVII МЕНДЕЛЕЕВСКАЯ ОЛИМПИАДА 2003 г. |
|
22 |
| I ТЕОРЕТИЧЕСКИЙ ТУР |
|
22 |
| II ТЕОРЕТИЧЕСКИЙ ТУР |
|
28 |
| XXXVIII МЕНДЕЛЕЕВСКАЯ ОЛИМПИАДА 2004 г. |
|
42 |
| I ТЕОРЕТИЧЕСКИЙ ТУР |
|
42 |
| II ТЕОРЕТИЧЕСКИЙ ТУР |
|
48 |
| XXXIX МЕНДЕЛЕЕВСКАЯ ОЛИМПИАДА 2005 г. |
|
66 |
| I ТЕОРЕТИЧЕСКИЙ ТУР |
|
66 |
| II ТЕОРЕТИЧЕСКИЙ ТУР |
|
71 |
| XL МЕНДЕЛЕЕВСКАЯ ОЛИМПИАДА 2006 г. |
|
89 |
| I ТЕОРЕТИЧЕСКИЙ ТУР |
|
89 |
| II ТЕОРЕТИЧЕСКИЙ ТУР |
|
95 |
| XLI МЕНДЕЛЕЕВСКАЯ ОЛИМПИАДА 2007 г. |
|
111 |
| I ТЕОРЕТИЧЕСКИЙ ТУР |
|
111 |
| II ТЕОРЕТИЧЕСКИЙ ТУР |
|
116 |
| XLII МЕНДЕЛЕЕВСКАЯ ОЛИМПИАДА 2008 г. |
|
133 |
| I ТЕОРЕТИЧЕСКИЙ ТУР |
|
133 |
| II ТЕОРЕТИЧЕСКИЙ ТУР |
|
139 |
| XLIII МЕНДЕЛЕЕВСКАЯ ОЛИМПИАДА 2009 г. |
|
153 |
| I ТЕОРЕТИЧЕСКИЙ ТУР |
|
153 |
| II ТЕОРЕТИЧЕСКИЙ ТУР |
|
159 |
| XLIV МЕНДЕЛЕЕВСКАЯ ОЛИМПИАДА 2010 г. |
|
175 |
| I ТЕОРЕТИЧЕСКИЙ ТУР |
|
175 |
| II ТЕОРЕТИЧЕСКИЙ ТУР |
|
181 |
| XLV МЕНДЕЛЕЕВСКАЯ ОЛИМПИАДА 2011 г. |
|
197 |
| I ТЕОРЕТИЧЕСКИЙ ТУР |
|
197 |
| II ТЕОРЕТИЧЕСКИЙ ТУР |
|
201 |
| XLVI МЕНДЕЛЕЕВСКАЯ ОЛИМПИАДА 2012 г. |
|
217 |
| I ТЕОРЕТИЧЕСКИЙ ТУР |
|
217 |
| II ТЕОРЕТИЧЕСКИЙ ТУР |
|
221 |
| XLVII МЕНДЕЛЕЕВСКАЯ ОЛИМПИАДА 2013 г. |
|
236 |
| I ТЕОРЕТИЧЕСКИЙ ТУР |
|
236 |
| II ТЕОРЕТИЧЕСКИЙ ТУР |
|
242 |
| XLVIII МЕНДЕЛЕЕВСКАЯ ОЛИМПИАДА 2014 г. |
|
254 |
| I ТЕОРЕТИЧЕСКИЙ ТУР |
|
254 |
| II ТЕОРЕТИЧЕСКИЙ ТУР |
|
259 |
| IL МЕНДЕЛЕЕВСКАЯ ОЛИМПИАДА 2015 г. |
|
271 |
| I ТЕОРЕТИЧЕСКИЙ ТУР |
|
271 |
| II ТЕОРЕТИЧЕСКИЙ ТУР |
|
276 |
| L МЕНДЕЛЕЕВСКАЯ ОЛИМПИАДА 2016 г. |
|
291 |
| I ТЕОРЕТИЧЕСКИЙ ТУР |
|
291 |
| II ТЕОРЕТИЧЕСКИЙ ТУР |
|
297 |
| LI МЕНДЕЛЕЕВСКАЯ ОЛИМПИАДА 2017 г. |
|
313 |
| I ТЕОРЕТИЧЕСКИЙ ТУР |
|
313 |
| II ТЕОРЕТИЧЕСКИЙ ТУР |
|
320 |
| LII МЕНДЕЛЕЕВСКАЯ ОЛИМПИАДА 2018 г. |
|
338 |
| I ТЕОРЕТИЧЕСКИЙ ТУР |
|
338 |
| II ТЕОРЕТИЧЕСКИЙ ТУР |
|
344 |
| LIII МЕНДЕЛЕЕВСКАЯ ОЛИМПИАДА 2019 г. |
|
361 |
| I ТЕОРЕТИЧЕСКИЙ ТУР |
|
361 |
| II ТЕОРЕТИЧЕСКИЙ ТУР |
|
368 |
Предисловие
Роль и значение химии в развитии современного общества трудно переоценить.
Неизменно актуальными остаются слова М.В. Ломоносова: «.Изучение химии имеет
двоякую цель: одна — усовершенствование естественных наук, другая - умножение
жизненных благ». Именно поэтому для школьников так важно научиться творчески
использовать полученные знания и умения по химии. Лучше всего свои способности
они могут проверить, участвуя в химических олимпиадах, поскольку олимпиадные
задачи - всегда неординарные задания. Для успешного выступления на олимпиаде
школьникам необходимы не просто химическая эрудиция, владение материалом на
уровне, превышающем уровень обычных школ, но и, что очень важно, химическая
интуиция, умение делать логические выводы, применять имеющиеся знания к новым,
подчас незнакомым областям химической науки.
Несмотря на многие кризисные явления, наблюдающиеся последние десятилетия в национальных системах образования не только стран СНГ, но также США и
многих стран Европы, предметные олимпиады школьников неизменно остаются одной из важнейших составляющих качественного школьного образования. Каждая
страна имеет сложившуюся многоуровневую систему национальных предметных
олимпиад, в том числе и по химии. Высшим уровнем химических олимпиад, своего
рода «чемпионатом мира» среди школьников по химии, является Международная
(«Всемирная») химическая олимпиада IChO. В команду для участия в Международной олимпиаде отбираются четыре сильнейших школьника каждой страны, ставшие
победителями национальных олимпиад. Эта система (национальная химическая
олимпиада - отбор участников на МХО из числа победителей национальных олимпиад и их дополнительная специальная подготовка - Международная олимпиада)
успешно функционирует и развивается в странах-участницах в течение многих лет
(подробнее о Всемирной химической олимпиаде см. сборник1). Однако наряду с этим
существует такое уникальное явление в области интеллектуальных соревнований
школьников, как Международная Менделеевская олимпиада школьников по химии.
Интересна сама история Менделеевских олимпиад. Дело в том, что химики оказались
единственными среди естественников, сумевшими сохранить традиции бывшей Всесоюзной олимпиады. Случилось так, что после распада СССР в 1992 г. Всесоюзная
химическая олимпиада продолжила свое развитие по двум направлениям: Всероссийская олимпиада (см. сборник2) и Международная Менделеевская олимпиада, в которой стали участвовать все страны — бывшие республики Советского Союза.
1Задачи Международных химических олимпиад. 2001 - 2003 / Под общ. ред. В.В. Еремина. М.: Иад-во «Экзамен», 2004. 416 с.
2Задачи Всероссийских олимпиад по химии / Под общ. ред. академика РАН, проф. В.В. Лунина. - М.: Изд-во «Экзамен», 2003. 480 с.
Менделеевская олимпиада проводится после распада СССР ежегодно. Первые,
самые тяжелые годы, - в России, но уже в 1997 г. олимпиада вновь перешагнула российские границы. В 2004 г. в 38-ой Менделеевской олимпиаде впервые приняли участие школьники Болгарии и Румынии, добившись при этом высоких результатов.
Позднее к олимпиаде присоединилось еще несколько стран, которые ежегодно принимают участие в этом соревновании. Рекордной по числу стран была олимпиада
2018 г., прошедшая в Минске.
Менделеевские олимпиады не только поддерживают общие высокие стандарты
химического образования в странах-участницах, но и несут важнейшую гуманитарную миссию, подтверждая, что у образования нет границ, что культура и традиции народов могут успешно дополнять и обогащать друг друга. Менделеевские олимпиады школьников являются мощным инструментом создания единого образовательного
пространства в странах-участницах. Значение Менделеевской олимпиады было подчеркнуто на Международном совещании по проблемам дальнейшего развития химических олимпиад (Рига, Латвия, 9-10 января 2004 г.), где было отмечено, что она является хорошим примером межрегионального сотрудничества и служит целям привлечения школьников к дальнейшему профессиональному изучению химии.
География Менделеевской олимпиады
|
|
Число |
Количество |
Год |
Город, страна проведения |
стран |
участников |
1992 |
Самара (Россия) |
9 |
200 |
1993 |
Пущино (Россия) |
4 |
29 |
1994 |
Пущино (Россия) |
9 |
43 |
1995 |
Пущино (Россия) |
11 |
63 |
1996 |
Пущино (Россия) |
12 |
85 |
1997 |
Ереван (Армения) |
8 |
48 |
1998 |
Иссык-Куль (Кыргызстан) |
12 |
68 |
1999 |
Минск (Беларусь) |
11 |
65 |
2000 |
Баку (Азербайджан) |
10 |
54 |
2001 |
Москва (Россия) |
13 |
80 |
2002 |
Алматы (Казахстан) |
14 |
85 |
2003 |
Пущино (Россия) |
12 |
76 |
2004 |
Кишинев (Молдова) |
14 |
77 |
2005 |
Душанбе (Таджикистан) |
15 |
87 |
2006 |
Ереван (Армения) |
15 |
82 |
2007 |
Минск (Беларусь) |
16 |
91 |
2008 |
Ташкент (Узбекистан) |
15 |
85 |
2009 |
Ашхабад (Туркменистан) |
13 |
87 |
2010 |
Баку (Азербайджан) |
14 |
87 |
2011 |
Москва (Россия) |
15 |
96 |
2012 |
Астана (Казахстан) |
18 |
112 |
2013 |
Ташкент (Узбекистан) |
17 |
118 |
2014 |
Москва (Россия) |
16 |
104 |
2015 |
Ереван (Армения) |
15 |
95 |
2016 |
Москва (Россия) |
21 |
114 |
2017 |
Астана (Казахстан) |
20 |
120 |
2018 |
Минск (Беларусь) |
22 |
135 |
2019 |
Санкт-Петербург (Россия) |
28 |
150 |
Жюри олимпиады и ее оргкомитет в разные годы возглавляли такие
известные ученые, как академики РАН А.Л. Бучаченко, Ю.А. Золотое и П.Д.
Саркисов, профессор Ю.А. Устынюк. С 1997 года оргкомитет олимпиады
возглавляет академик РАН В.В. Лунин. Важную работу с командами
осуществляют члены оргкомитета профессор Н.Е. Кузьменко и доцент О.Н.
Рыжова. С 2002 года работу жюри и методической комиссии олимпиады
координирует заведующий кафедрой органической химии МГУ, профессор
В.Г. Ненайденко. В состав оргкомитета, Методической комиссии и жюри
олимпиады входят профессора и преподаватели ведущих вузов, а также
учителя химии общеобразовательных школ стран-участниц. Перечислим
имена членов жюри - авторов задач Менделеевской олимпиады, начиная с
2002 года: Аббасов В.М., Аббасов М.М., Андриуцэ Е.Н., Апяри В.В.,
Асаченко А.Ф., Багдасарян Д.А., Бахтин С.Г., Беклемишев М.К., Белых З.Д.,
Беркович А.К., Бибин А.В., Борщевский А.Я., Будынина Е.М.,
Волочнюк Д.М., Гарифуллин Б.Н., Гармаш А.В., Гладилин А.К.,
Головко Ю.С., Горлова А.А., Гулевич (Сырлыбаева) Д.Г.,
Дильмухамбетов Е.Е., Дубенский А.С., Еремин В.В., Жиентаев Т.М.,
Жиров А.И., Заборова О.В., Зайцев А.А., Иванов Д.Т., Иванова О.А.,
Иоффе И.Н., Калугин С.Н., Кандаскалов Д.В., Карпова Е.В., Карпушкин Е.А.,
Катаев Е.А., Кебец П.А., КисинА.В., Кузин СВ., Кулаго А.А.,
Кутанова О.А., Лиханов М.С, Лукьянова М.А., Мажуга А.Г., Малинина
(Олейник) Л.И., Маринчук А.И., Матусевич О.В., Медведев Ю.Н., Мелик-Нубаров Н.С., Мухтаров Ф.Ш., Назаров И.Г., Ненайденко В.Г.,
Никитина В.Н., Новиков Ф.Н., Павлечко Е.В., Панин Р.В., Плодухин А.Ю,
Предеус А.В., ПутляевВ.И., Ревенко М.Д., РешетоваМ.Д., Розанцев Г.М.,
Семенов С.Е., Серяков С.А., Скобелева В.Б., СмурныйЕ.Д., Сычев Ю.Н.,
Тимковский И.И., Ткаченко С.Е., Трушков И.В., Туков А.А., Устынюк Ю.А., Федотов С.С, Хвалюк В.Н., Чернов О.В., Чулкин П.В., Чуранов С.С. ,
Шварцман В.Е., Швед A.M., Швед Е.Н., Яблоцкий К.В., Язев О.В.,
Якимов А.В.
У Менделеевской олимпиады есть отличительная черта - в составе ее Методической комиссии и в жюри наряду с профессорами и преподавателями обязательно
работают студенты и аспиранты — вчерашние победители Менделеевских олимпиад:
это помогает сохранить традиции и обеспечивает преемственность на годы вперед. На
сегодняшний день Сергей Кузин и Андрей Швед - студенты химического факультета
МГУ, Даяна Гулевич - аспирант химического факультета МГУ, Максим Лиханов -
кандидат химических наук, сотрудник химического факультета МГУ, а Филип Илиевски - аспирант ЕТН (Цюрих, Швейцария).
Финансирование олимпиады все годы проводилось на спонсорские средства
различных финансовых структур и фирм. С 1997 г. значительную часть расходов по
проведению олимпиады брали на себя также Правительства стран, которые принимали олимпиады.
В олимпиаде принимают участие школьники выпускных и предвыпускных
классов школ из числа победителей национальных химических олимпиад. Важно
подчеркнуть, что вместе со школьниками на олимпиаду приглашается руководитель;
как правило, это вузовский преподаватель - «тренер» команды. Именно он имеет
возможность, при необходимости, накануне каждого тура олимпиады сделать перевод
заданий на национальный язык. Кроме того, по желанию участников им предлагаются
задания олимпиады на английском языке. Все участники олимпиады, независимо от
того, в каком классе они учатся, выполняют одно и то же задание. Традиционно
олимпиада состоит из трех туров: первый теоретический тур (8 обязательных задач),
второй теоретический тур (5 задач из 15 по выбору участников) и экспериментальный
тур. Задачи первого тура по сложности соответствуют программе специализированных химических классов, на втором туре предлагаются задачи несколько более высокого уровня. Задачи второго тура разделены на пять разделов: аналитическая химия,
неорганическая химия, органическая химия, науки о живом и физическая химия (по 3
задачи в каждом разделе). Участники олимпиады должны выполнить 5 задач, при
этом - не более двух задач из одного раздела3, таким образом, проверяется универсальность подготовки участника. Третий экспериментальный тур олимпиады подразумевает наличие у школьников навыков работы в химической лаборатории. Задание третьего тура разрабатывается таким образом, чтобы участники могли продемонстрировать умение выполнять химический анализ веществ, а также проводить синтез по
предложенной методике.
3Это правило впервые было введено на 37-ой ММО
На первом теоретическом туре последние годы участникам предлагают решить
8 задач по 10 баллов каждая, при этом учитываются все задачи комплекта. Соответственно, максимальная оценка за первый тур - 80 баллов. Задания второго тура (часто
именуемого «туром по выбору») разделены на 5 разделов (аналитическая химия,
науки о живом и полимеры, неорганическая химия, органическая химия, физическая
химия). В каждом разделе представлено по 3 задачи стоимостью по 15 баллов. Участникам предлагается выбрать и решить наиболее подходящую им задачу. Естественно,
они могут решить и большее количество задач, но учитываются только 5 задач, по
одной, наиболее успешно выполненной, из каждого раздела. Максимальная оценка за
второй тур - 75 баллов. Продолжительность каждого теоретического тура составляет
5 часов.
На теоретических турах каждому участнику предоставляют брошюру с задания
и периодической системой Д.И. Менделеева, листы ответов, тетрадку-черновик и
ручку. Листы ответов не подписываются, поскольку по окончании тура работы шифруются, а международное жюри проводит проверку анонимно.
Экспериментальный тур, обычно проводящийся после дня отдыха, как правило,
включает две задачи, чаще всего, аналитическую и синтетическую. На экспериментальном туре, помимо непрограммируемого калькулятора, участники обязаны иметь
при себе лабораторный халат и защитные или корректирующие очки. Максимальная
оценка за этот тур - 75 баллов, продолжительность составляет от 4 до 5 часов в зависимости от сложности задания. Таким образом, максимальная суммарная оценка за
все туры - 230 баллов.
В процессе проведения туров участникам запрещается приносить с собой любую литературу, вычислительные средства (кроме калькулятора), пользоваться мобильными телефонами и прочими средствами связи, общаться с соседями, мешать
своими действиями другим участникам. За нарушение правил участник может быть
дисквалифицирован.
По окончании теоретических туров и проверки проводится показ работ, в ходе
которого сами участники (а не их руководители!) могут уточнить у членов международного жюри интересующие их вопросы и даже выразить свое несогласие с выставленной оценкой. В ряде случаев школьникам удается убедить маститых ученых в своей правоте, в связи с чем результаты изначальной проверки пересматриваются.
В завершение работы, международное жюри определяет границы медалей различного достоинства. Согласно Положению о ММХО, золотые медали получают 10,
серебряные - 20, а бронзовые - 30% от общего числа участников.
Международная Менделеевская химическая олимпиада школьников имеет ряд
существенных отличий от Международной и большинства национальных химических
олимпиад. К числу основных следует отнести отсутствие программы и подготовительного комплекта заданий, в связи с чем участники должны хорошо ориентироваться в различных областях химии. Задания ММХО готовит постоянно действующая
Методическая комиссия, в состав которой входят ведущие ученые и педагогихимики, представляющие страны-участницы олимпиады. Официальные рабочие языки ММХО - русский и английский. При желании руководители команд могут переводить задания на родной язык.
Международная Менделеевская химическая олимпиада (ММХО) школьников
является преемницей Всесоюзной химической олимпиады, зародившейся более 50 лет
назад в Советском союзе. Замышлявшаяся в начале 1990-х как соревнование лучших
химиков независимых государств -бывших союзных республик СССР, за последнее
десятилетие олимпиада существенно расширила географию. Тем не менее, она до сих
пор остается региональным соревнованием, в котором участвуют порядка 25 стран.
Каждый год через два-три месяца после ММХО лучшие химики мира традиционно
собираются на Международную химическую олимпиаду (МХО), в которой в настоящее время принимают участие порядка 300 школьников из почти 80 стран, представляющих все обитаемые континенты Земли.
Традиционно многие победители, призеры и просто участники ММХО отбираются в состав сборных своих стран для участия в МХО, в связи с чем педагогическая
общественность разных стран из года в год обсуждает один и тот же вопрос: в какой
из этих олимпиад тяжелее добиться успеха? Вопрос не праздный, поскольку у ММХО
и МХО, действительно, много различий. К их числу можно отнести существенно
(примерно в 2,5 раза) большее число участников МХО; отсутствие предметной программы ММХО, в связи с чем на этом соревновании в задачах может появиться «любая» химия, а на МХО - только темы, заранее анонсированная в подготовительном
комплекте заданий; ММХО включает два теоретических тура, а МХО - один; в МХО
Научный комитет формируется страной-хозяйкой олимпиады, в связи с чем он каждый год меняется, а в ММХО функционирует постоянно действующая Методическая
комиссия... И это далеко не все отличия!
Корреляция результатов на ММХО и МХО
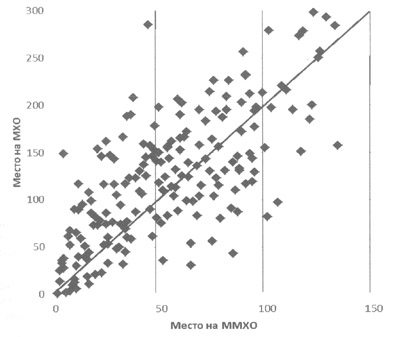
Рис. 1. Анализ выступления школьников на ММХО и МХО одного и того же
года проведения. По оси абсцисс отложено место участника в ММХО, по оси
ординат - место того же участника в МХО. Результаты относятся к
олимпиадам 2016-2018 годов.
Так какая же олимпиада сложнее? Сравнение результатов школьников (2016-
2018 гг.), участвовавших в один и тот же год в ММХО и МХО, представлено на рис.1.
Каждая точка на диаграмме отображает одного участника. Анализ распределения
точек на диаграмме указывает на явную корреляцию результатов на двух олимпиадах.
В подавляющем большинстве случаев школьники подтверждают на МХО свое относительное место, завоеванное на ММХО. Случаи удачного выступления на одной из
олимпиад и неудачного на другой редки, а, если и случаются, то в основном относятся к менее удачному выступлению на МХО, чем на ММХО. Возможная причина данного явления заключается в том, что многие традиционно сильные команды представлены на ММХО более чем 4 участниками (вплоть до 10), а состав команд на МХО
не может превышать 4 человек. В результате этого значительное количество сильных
школьников, зачастую даже с золотыми и серебряными медалями ММХО, не может
попасть в команду на МХО из указанного выше лимита.
Выявленные выше тенденции при сравнении мест участников находят
подтверждение по результатам анализа медальных достижений школьников
(рис. 2). Так, более половины всех участников получили на ММХО и МХО медали одинакового достоинства. При этом следует отметить, что доля
медалей того или иного достоинства от общего числа участников на обеих
олимпиадах практически одинаковая. Доля участников, «перескакивающих»
в соседнюю медальную категорию хотя и значительно меньше, но тоже
существенна, а вот «прыжки» через две или три категории наблюдаются
крайне редко.
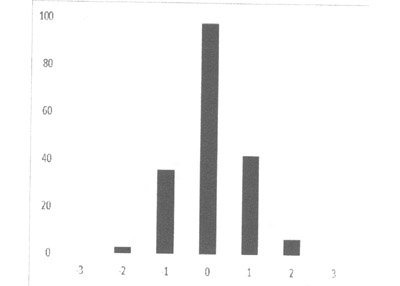
Рис. 2. Количество участников, подтвердивших, улучшивших и ухудшивших
медальный результат на МХО по сравнению с ММХО того же года. «О» -
подтверждение, отрицательные значения - ухудшение, положительные
значения - улучшение категории. Категории: «Золото», «Серебро», «Бронза»,
участник (немедалист). Приведены данные за 2016-2018 гг.
Особо следует подчеркнуть, что за последние три года дважды
абсолютный победитель ММХО занимал первое место и в МХО. В 2016 году
отличился Андрей Илиеску из Румынии, а в 2017 - Александр Жигалин из
России.
Таким образом, и ММХО, и МХО относятся к наиболее интересным,
сложным и престижным химическим олимпиадам, стать победителем каждой
из которых крайне сложно и, в то же время, почетно! Все вышеизложенное
показывает уникальность положения Менделеевской олимпиады в системе
химических олимпиад высокого уровня.
В предлагаемой вашему вниманию книге представлены обработанные составителями уникальные материалы - теоретические задания, решения и статистические
данные Менделеевских олимпиад с 2002 г. Эти материалы представлены таким образом, что любую задачу можно использовать отдельно для подготовки школьника или
студента. Задачи носят комплексный характер и расчитаны на универсальную подготовку читателя.
|




