Решение варианта 1

1. Т (лед) = Т (вода, ж); Р (лед) = Р (вода, ж);  (лед) =   (вода, ж).

2.

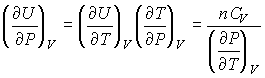
3.

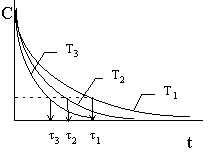
Для определения энергии активации Е_А можно использовать зависимость времени превращения одной и той же части вещества А, например ₁,  ₂ и   ₃, (начальные концентрации вещества А при всех Т должны быть одинаковы, за исключением реакций первого порядка) от температуры: ln  _{(1/n )} = А + В/Т, где А постоянная, а В = Е_А/R.

4. Используем уравнение изотермы химической реакции:
_rG'⁰ =  _rG⁰ + RT ln a _H+;
RT ln a _H+ = - 2.303^. RT pH.
_rG⁰ =  _rG'⁰ + 2.303^. RT pH,  где _rG⁰ - стандартная энергия Гиббса реакции (в качестве стандартного состояния выбрана единичная концентрация в моль/л, т.е. все с_i и _i равны 1). 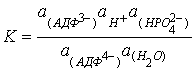, где а - активности реагентов.

5. Например, Pt | Ag | AgCl | КCl (водный р-р) || КОН (водный р-р) | О₂ | Pt

Реакция в электрохимической цепи:

0,5О₂ + Н₂О + 2Cl-  + 2Ag = 2AgCl + 2ОН-  , E⁰ = -   _rG⁰/nF = -   _rG⁰/2F

D _rG⁰ = 2 _fG⁰ (AgCl) + 2 _fG⁰ (ОН-  ) -   _fG⁰ (Н₂О) -  2 _fG⁰ (Cl- ) , причем

можно использовать _fG⁰ при 298 К.

6.   = cRT (1), P_i = c_iRT (2). Нет, так как уравнение (1) выведено для малых концентраций растворенного вещества и в идеальных жидких растворах есть межмолекулярное взаимодействие.

7.  _rН⁰₂₉₈ = 2 _fН⁰ (С₂Н₅ОН (ж)) + 2 _fН⁰_i (СО₂) -   _fН⁰_i (С₆Н₁₂О₆ (тв))

  _rН⁰₂₉₈ = - 66.33 кДж/моль. а) Если _rН⁰ <  0, то константа равновесия уменьшится с увеличением температуры согласно уравнению изобары Вант-Гоффа: .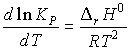
б) Давление не влияет на значение константы равновесия: RT ln K_P = - _rG⁰.

[содержание]

Решение варианта 2

1.

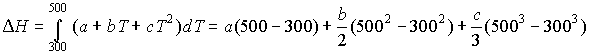
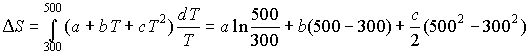
2. Экспериментально определяют теплоту сгорания при постоянном объеме Q_V, причем Q_V =  U . Реакция: С₁₂Н₂₂О₁₁ (тв)+ 12О₂ = 12СО₂ + 11Н₂О (ж)

Для этой реакции U    Н . _сН⁰ - энтальпия сгорания 1 моля вещества, следовательно _сН⁰ = (4 ккал/г)^. М (г/моль), где М - молярная масса сахара.

3. U =  + TS - PV

4. Опытная энергия активации при низких температурах положительна, а при высоких температурах отрицательна. В случае ферментативных реакций увеличение температуры может приводить к денатурации фермента и, следовательно, к уменьшению эффективной константы скорости реакции.

5. Если считать, что соль полностью диссоциирована, то  = 2cRT, следовательно с =  /2RT, причем с - в моль/л.

6. 1) Pt | СН₃С(=О)Н, Н⁺, С₂Н₅ОН || НАД⁺, Н⁺, НАДН | Pt

2) 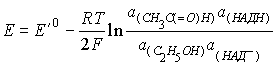, где E^'0 = Е'⁰ (1) -  Е'⁰ (2)

3) ln K_a = nFE^'0/RT

4) при 298 К. Рассчитав Е⁰, можно рассчитать _rG⁰ : _rG⁰ = - nFE⁰ = - 2FE⁰.

7. Применяем уравнение изотермы химической реакции:

D _rG_Р,Т =  _rG⁰_Т + RT ln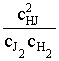 и  _rG⁰_Т = - RT ln K_P. Для этой реакции К_P = К_C.

1)  _rG_Р,Т = RT (ln 5²/0.5^.0.25 -  ln 50) = RT (ln 200 -  ln 50) >  0, следовательно, образование HJ не пойдет.

2) _rG_Р,Т = RT (ln 10²/2^. 1 -  ln 50) = RT (ln 50 -  ln 50) = 0, следовательно система находится в равновесии и образование HJ не пойдет.

[содержание]

Решение варианта 3

1. При использовании определения энергии Гиббса G = U -  TS + pV и уравнения, обобщающего первый и второй законы термодинамики dU = TdS -  pdV можно получить фундаментальное уравнение для энергии Гиббса dG = - SdT + Vdp. Отсюда видно, что первая производная энергии Гиббса по давлению равна: (dG/dp)_T = V. При интегрировании получаем искомую зависимость G(Р₂) = G(Р₁) + Vdp. В случае абсолютно твердого тела V = const и можно записать G(Р₂) = G(Р₁) + V(Р₂ - Р₁).

2. Энергией Гиббса образования называют изменение энергии Гиббса в реакции образования одного моля данного вещества из простых веществ в наиболее стабильной модификации при Р = 1 атм. Для ее расчета необходимо знать энтальпию и энтропию реакции образования, то есть, другими словами, энтальпию и энтропию образования, _fG =  _fH -  T  _fS. Энтальпию образования можно определить из энтальпий сгорания по известному соотношению, _fH =   _cH_i,ИСХОД -    _cH_j,ПРОД. Энтропию образования можно рассчитать из абсолютных энтропий,

D _fS = S_i,ПРОД - S_j,ИСХОД.

3. Вначале рассчитаем стандартную энергию Гиббса для реакции A' = A", _rG⁰ = ( _fH⁰_A" - _fH⁰_A') - T (S⁰_A" - S⁰_A') при данной температуре. Теперь надо записать, каким образом энергия Гиббса реакции зависит от давления. С использованием результатов задачи N1 в приближении независимости объема от давления можно записать _rG(Р) = _rG⁰ + _rV(Р - Р⁰). При равновесии _rG должна быть равна нулю. Отсюда получаем

p = p⁰ - _rG⁰/ _rV, _rV=М(1/ І -1/ ў ), где М - молярная масса вещества.

4. Согласно критерию равновесия химический потенциал чистого растворителя при атмосферном давлении должен быть равен химического потенциалу растворителя в растворе при повышенном давлении, ⁰₁ = ₁(Р + ), где - осмотическое давление. Можно записать, что

m ₁(Р + ) = ⁰₁ + RT ln a₁ + dР (где - парциальный мольный объем растворителя при заданной концентрации). Если концентрация растворенного вещества невелика, то можно приближенно принять парциальный мольный объем растворителя равным мольному объему чистого растворителя, и тогда мы получаем уравнение для определения активности растворителя RT ln a₁ = - V . Активность растворенного вещества можно определить по уравнению Гиббса-Дюгема.

5. Степень диссоциации газа связана с константой равновесия реакции AB = A + B, K_Р =  ²Р_ОБЩ./{(1 +  )(1 -   )Р_СТАНД.}. При увеличении температуры константа равновесия меняется в соответствии с изобарой Вант-Гоффа (d ln K_Р/dT) = _rH⁰/(RT²). Энтальпия реакции диссоциации положительна, следовательно константа равновесия будет возрастать при увеличении температуры, а это в свою очередь приведет к увеличению степени диссоциации при постоянном давлении.

6. ЭДС элемента связана с энергией Гиббса химической реакции по уравнению _rG = - nEF, где F - число Фарадея, а n - число переносимых электронов. В случае записанной реакции n = 2. Можно записать, что E = - _rH/(nF) + T _rS/(nF). Тогда ЭДС при другой температуре можно определить по уравнению E₂ = E₁ + (T₂ - T₁) _rS/(nF), а энтропию реакции можно определить из данных при температуре T₁, _rS = ( _rH + nE₁F)/T₁.

7. Время полупревращения связано с константой скорости по уравнению:

t _1/2 = 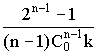, где n - порядок реакции, k - константа скорости, а C_o - начальная концентрация. Если можно считать, что 1) порядок реакции не меняется с изменением температуры (механизм реакции один и тот же),

2) эксперименты проведены при одной и той же начальной концентрации (C_o = const), то мы получаем, что при этих условиях ln k ~ -  ln  _1/2, и

E_A = - RT²(d ln _1/2/dT) соответственно.

[содержание]