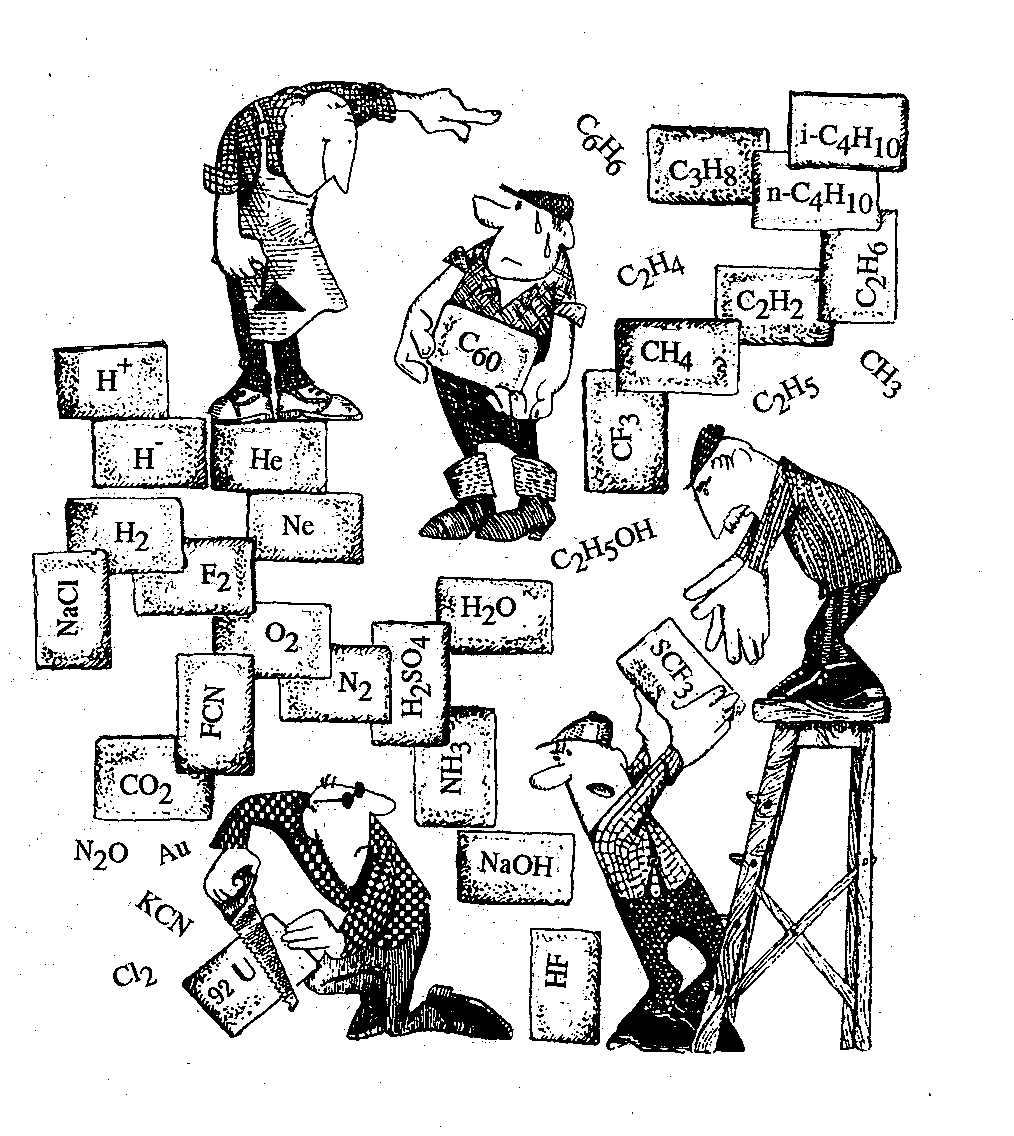
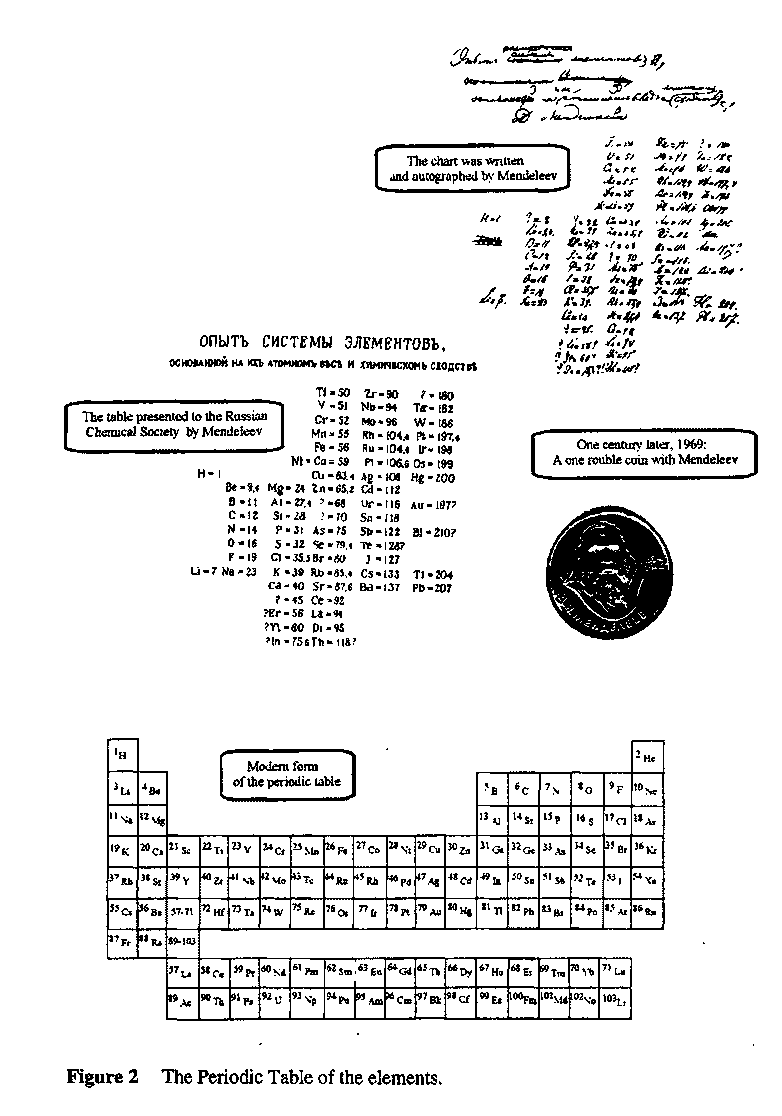
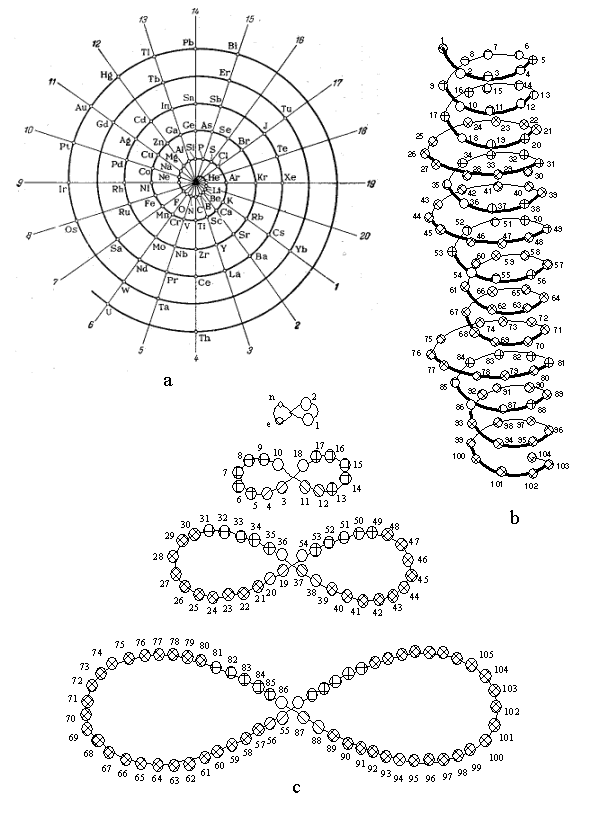
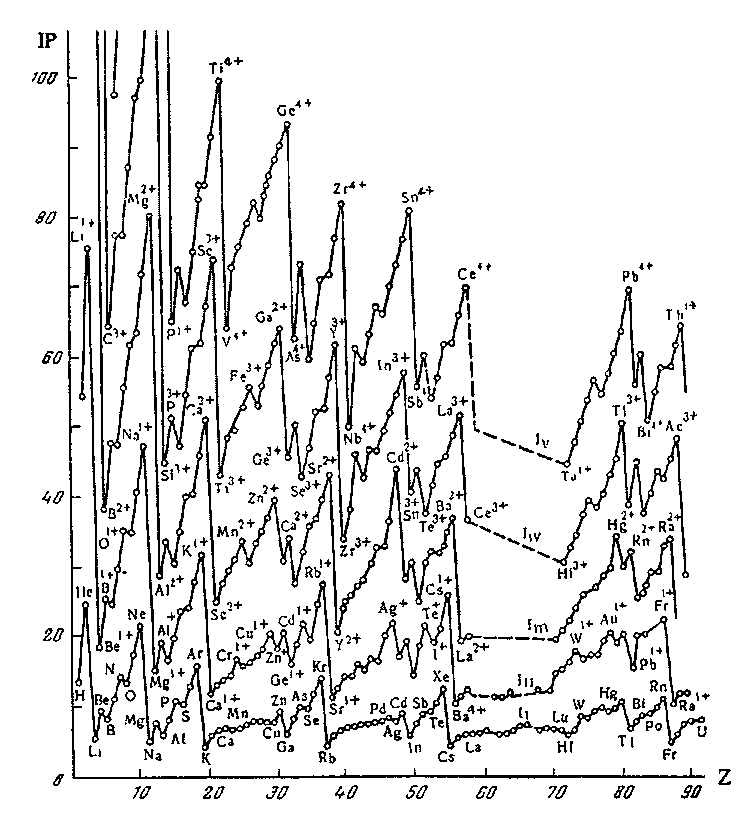
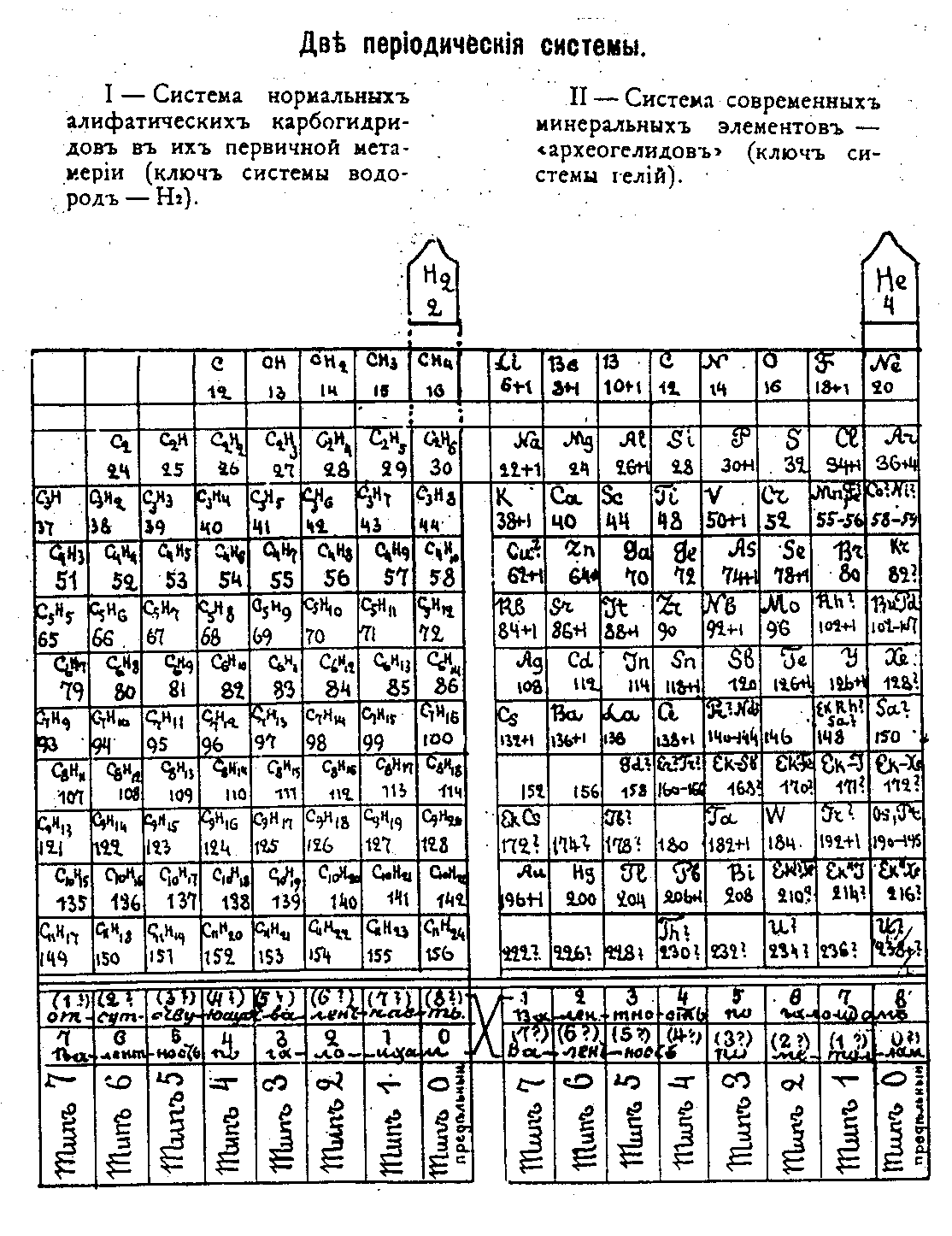
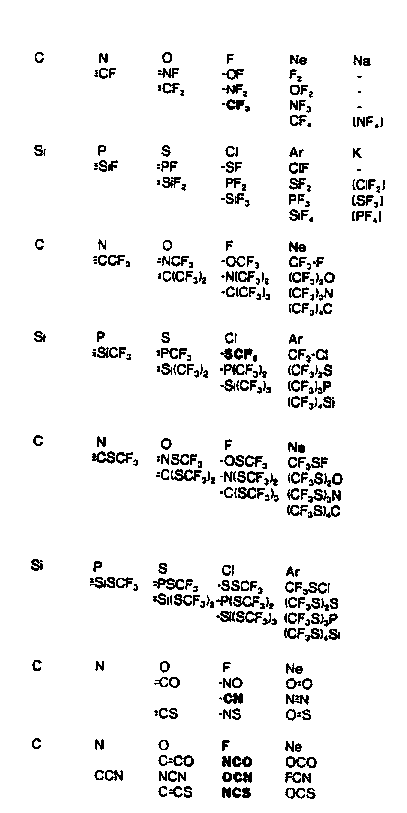
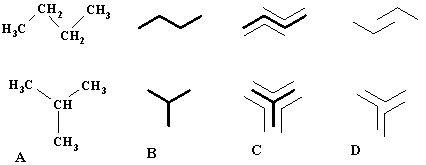
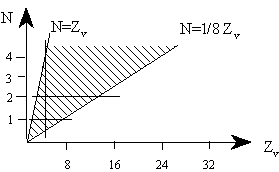
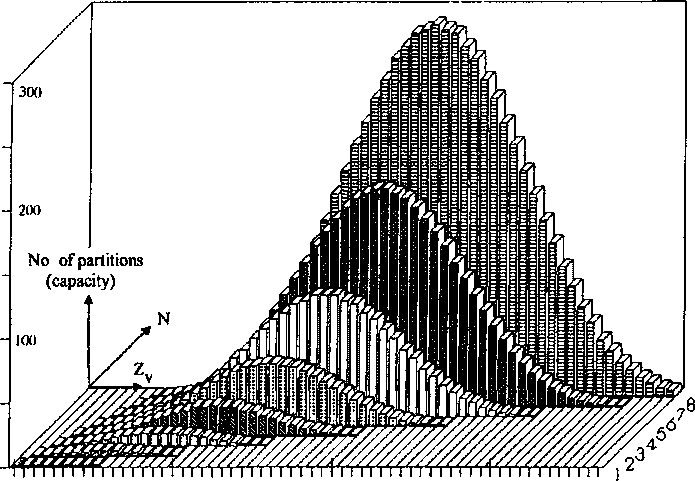
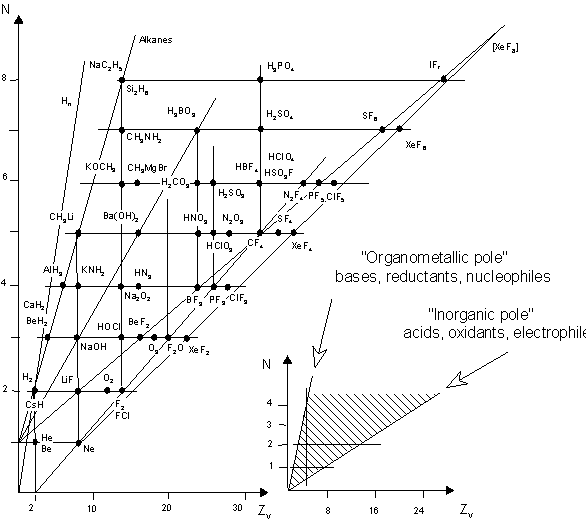
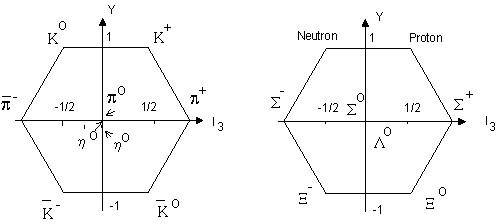1. (a) J. W. Dobereiner, Poggend. Ann., 15, 301 (1829); (b)
J. W. Dobereiner, Ostwald's Klassiker, 66, Leipzig, 1895.
2. J. W. Van Spronsen, The Periodic System of Chemical Elements, Elsevier:
Amsterdam, 1969.
3. E. G. Mazurs, Graphic Representations of the Periodic System during
One Hundred Years, University of Alabama Press: University, AL, 1974.
4. V. I. Semishin, Literature on Mendeleev's Periodic Law: 1869-1969,
Vysshaya Shkola Publ.: Moscow, 1969 (in Russian).
5. W. Odling, Phil. Mag., 4 (13), 423, 480 (1857).
6. B. de Chancourtois, Compt. Rend. 54, 757, 840, 967 (1862);
ibid.
55,
600 (1862).
7. (a) L. Meyer, Modern Theories of Chemistry, Breslau, 1864 (in German);
English translation Longman: London, 1888; (b) J. L. Meyer, Liebig's Ann.,
Suppl. 7,
354 (1870); (d) L. Meyer und D. Mendelejeff (in German), Ostwald's
Klassiker, 68, 3-te Aufl., Leipzig, 1913.
8. (a) J. A. R. Newlands, Chem. News, 7, 59 (1863); ibid.
12,
83 (1865); ibid. 13, 113 (1866); (b) J. A. R. Newlands, On
the Discovery of Periodic Law and on Relations among Atomic Weights, London,
1884; (c) W. Taylor, J. Chem. Educ., 26, 491 (1949).
9. (a) D. I. Mendeleev, J. Russ. Chem. Soc., 1 (2-3), 35, 60
(1869); ibid. 3 (2), 25 (1871); (b) D. I. Mendelejeff, Ber.,
2,
553 (1869); ibid. 3, 990 (1870); ibid. 4, 990
(1871); Liebig's Ann. Suppl. 8, 133 (1872); (c) D. I. Mendeleev,
Melanges phys. et. chim., 7, 445 (1871); (d) D. I. Mendeleev, J.
Chem. Soc., 55, 634 (1889); (e) D. I. Mendeleev, Principles of Chemistry,
St. Petersburg, 1869-71 (in Russian), English translation Longmans: London,
1897.
10. (a) B. M. Kedrov, Microanatomy of the Great Discovery, Nauka Publ.:
Moscow, 1970 (in Russian); (b) N. A. Figurovskii, Discovery and Confirmation
of Mendeleev Periodic Law, Znaniye Publ.: Moscow, 1969 (in Russian); (c)
B. M. Kedrov, Forecasts of Mendeleev in Atomistics: Unknown Elements, Atomizdat
Publ.: Moscow, 1977 (in Russian); (d) B. M. Kedrov, Forecasts of Mendeleev
in Atomistics: Atomic Weights and Periodicity, Atomizdat Publ.: Moscow,
1978 (in Russian).
11. D. N. Trifonov, On Quantitative Interpretation of Periodicity, Nauka
Publ.: Moscow, 1971 (in Russian).
12. V. I. Semishin, Periodic System of Chemical Elements, Khimija Publ.:
Moscow, 1972 (in Russian).
13. J. Avotins, Is the Chemistry Incomprehensible? Zinatne: Riga, 1987
(in Latvian).
14. H. Baumgauer, Relation between Atomic Weights and Nature of Chemical
Elements, Braunschweig, 1870 (in German).
15. A. Bilecki, Reflection about the Periodic System of Chemical Elements,
Troppau, 1915 (in German).
16. H. Basset, Chem. News, 65 (3-4), 19 (1892).
17. R. T. Sanderson, Chemical Periodicity, Reinhold Publ.: NY, 1960.
18. (a) R. Rich, Periodic Correlation, W. A. Benjamin: NY, 1965; (b)
R. J. Puddefat, The Periodic Table of the Elements, Carendon: Oxford, England,
1972.
19. (a) B. M. Kedrov, D. N. Trifonov, Law of Periodicity and Chemical
Elements, Nauka Publ.: Moscow, 1969 (in Russian); (b) D. N. Trifonov, Structure
and Boundaries of the Periodic System, Gosatomizdat Publ.: Moscow, 1969
(in Russian); (c) K. V. Astakhov, Modern State of the Mendeleev Periodic
System, Znaniye Publ.: Moscow, 1969 (in Russian).
20. (a) K. Saito, Chemistry and Periodic Table, Shoten Publ.: Iwanami,
1979; (b) Doctrine of Periodicity: History and Modernity, Nauka Publ.:
Moscow , 1981 (in Russian); (c) Evolution of Mendeleev's Ideas in Modern
Chemistry, Nauka Publ., Leningrad, 1984 (in Russian).
21. (a) P. E. Lecoq de Boisbaudran, Compt. Rend., 81, 493 (1875);
ibid.82,
1036 (1876); ibid. 83, 611 (1876); (b) D. I. Mendeleev,
ibid.81,
969 (1875).
22. (a) L. F. Nilson, Compt. Rend., 88, 645 (1879); (b) P. T.
Cleve, Chem. News, 40, 159 (1879); (c) D. I. Mendeleev, J. Russ.
Phys. Chem. Soc., 13 (8), 517 (1881).
23. (a) C. Winkler, Ber., 19, 210 (1886); ibid. 30,
15 (1897); (b) C. Winkler, J. Prakt. Chem., 34, 177 (1887).
24. W. Ramsay, in Brit. Ass. Adv. Sci., Toronto, 1897, p. 3; .
25. (a) W. Ramsay, in Nobel Lect. Chem. (1901-1921), Stockholm, 1966,
p. 72; (b) W. Ramsay, M. W. Travers, Proc. Roy. Soc., 63, 405, 437
(1898); (c) M. W. Travers, The Discovery of the Rare Gases, Arnold: London,
1928.
26. B. F. Brauner, Berlin. Ber., 2, 872 (1878); ibid.14,
53 (1881).
27. (a) L. F. Nilson, O. Petersen, Berlin. Ber., 17, 995 (1884);
(b) idem., Ber., 17, 987 (1884).
28. D. I. Mendeleev, Bull. Acad. Sci. St. Petersburg, 8, 45 (1871).
29. (a) B. F. Brauner, Sitzungs Ber. Acad. Wiss. (Wein), 92,
814 (1881); (b) P. T. Cleve, Ber., 8, 128 (1875); (c) C. Rammelsberg,
ibid.5,
1003 (1872); (d) H. E. Roscoe, ibid. 7, 1131 (1874).
30. (a) A. van den Broek, Ztschr. Phys., 14, 32 (1913); (b) H.
Mosely, Phil. Mag., 6 (26), 1024 (1913); ibid. 6 (27),
703 (1914).
31. (a) A. A. Lyubischev, On the Form of the Natural System of Organisms,
Biological Institute Proceeedings, Perm' University Publ.: Perm', 2
(3), 99 (1923) (in Russian); (b) A. A. Lyubischev, in Problems of Evolution,
Part 1, Nauka Publ.: Novosibirsk, 1968, p. 7 (in Russian); (c) A. A. Lyubischev,
in Applied Mathematics in Biology, Nauka Publ.: Moscow, 1979, p. 12 (in
Russian).
32. (a) A. A. Lyubischev, Biometrics, 18 (4), 455 (1962); (b)
A. A. Lyubischev, Evolution, 17 (4), 414 (1963), (c) A. A. Lyubischev,
Ann. Rev. Entomol., 14, 19 (1969); (d) A. A. Lyubischev, Russ. J.
Gen. Biol., 38 (2), 245 (1977).
33. (a) S. White, New Scientist, 66 (951), 513 (1975); (b) D.
Granin, ibid. 68 (980), 705 (1975); (c) S. V. Meyen, B. S.
Sokolov, Yu. A. Shreyder, Classical and Non-classical Biology: Phenomena
of Lyubischev, Acad. Sci. USSR Bull., Moscow, 1977, Vol. 10, p. 112 (in
Russian).
34. Yu. A. Urmantsev, Russ. J. Gen. Biol., 37 (2), 216 (1976);
ibid.39
(5), 699 (1978); ibid. 40 (3), 351 (1979).
35. (a) Yu. A. Urmantsev, in Symmetry, Unifuing Human Understanding,
Ed. I. Hargittai, Pergamon Press: New York, Oxford, 1986 p. 379; (b) Yu.
A. Urmantsev, Symmetry of Nature and Nature of Symmetry, Mysl' Publ.: Moscow,
1974 (in Russian); (c) System, Symmetry, Harmony, Eds. V. S. Tukhtin, Yu.
A. Urmantsev, Mysl' Publ.: Moscow, 1988 (in Russian).
36. (a) D. Rouvray, Chem. Soc. Rev., 3, 335 (1974); (b) D. Rouvray,
in Chemical Information Systems: Beyond the Structure Diagram, Eds. D.
Bawden, E. Mitchell, Ellis Horwood: New York, London, 1991, p. 124.
37. Z. Slanina, Contemporary Theory of Chemical Isomerism, Academia:
Prague, 1986.
38. V. B. Kasinov, Biological Isomerism, Nauka Publ.: Leningrad, 1973
(in Russian).
39. S. M. Polikanov, Isomerism of Forms of Atomic Nuclei, Atomizdat
Publ.: Moscow, 1977 (in Russian).
40. (a) J. J. Berzelius, Jahresber., Tubingen, 20 (2), 13 (1840);
(b) W. E. Addison, The Allotropy of the Elements, Oldsborne Press: London,
1964.
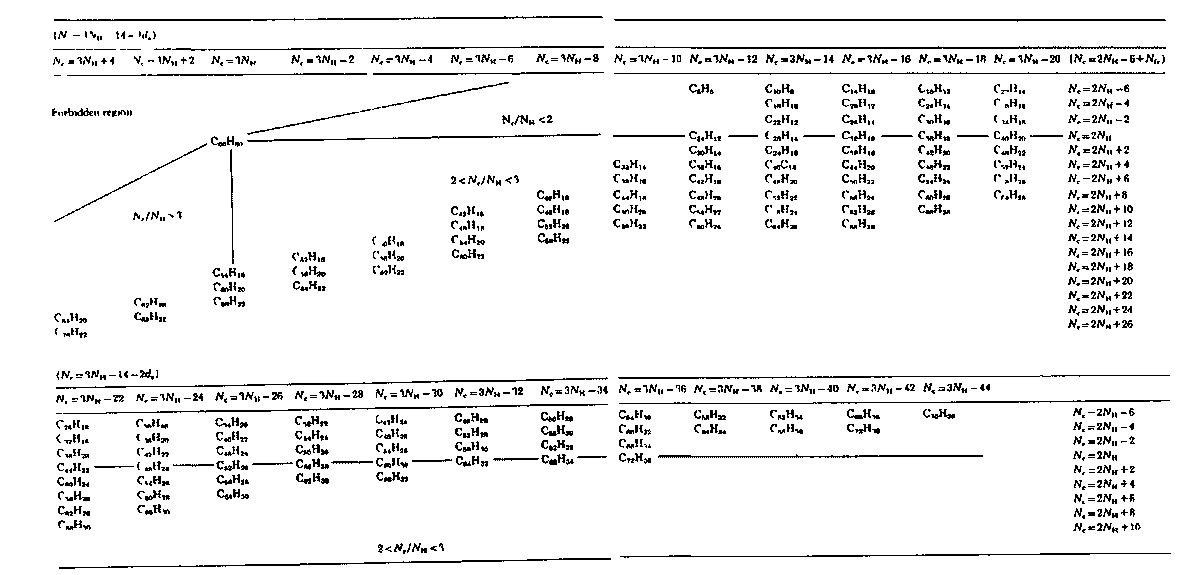
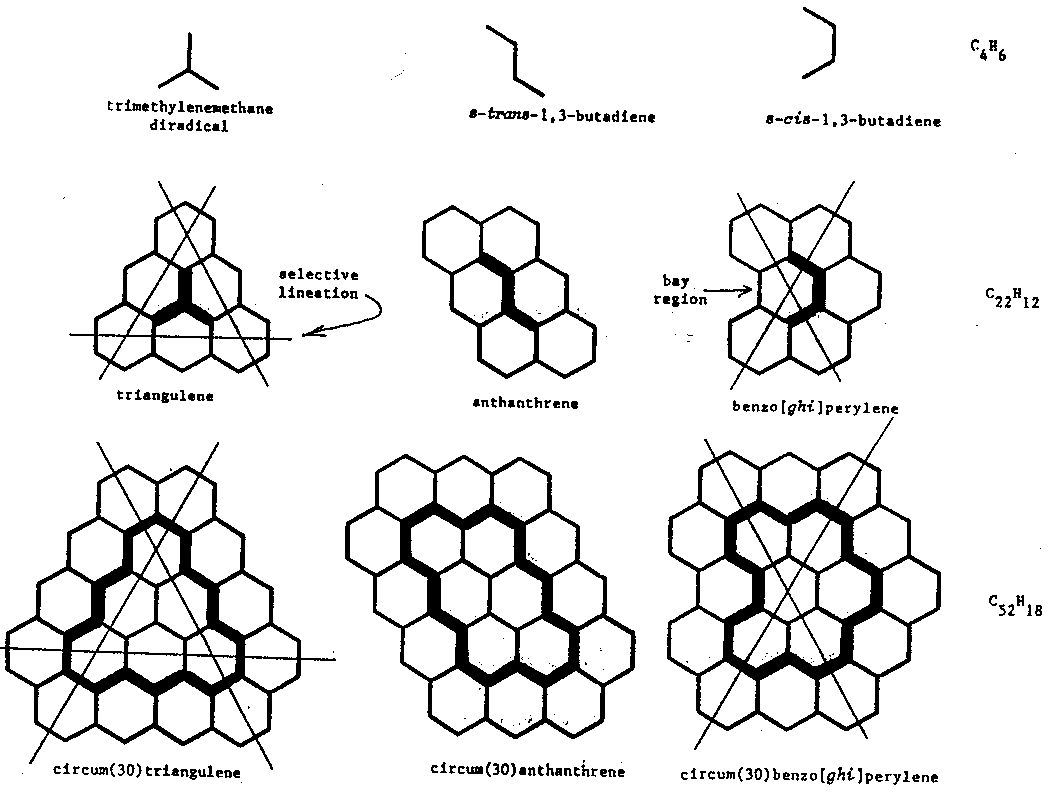
41. (a) J. R. Dias, Acc. Chem. Res. 18, 241 (1985), (b) J. R.
Dias, Handbook of Polycyclic Hydrocarbons, Parts A and B, Elsevier: New
York, 1987 and 1988.
42. R. Hefferlin, in Proc. Intern. Confer. Society of General System
Research, May 27-31, 1985, Ed. B. H. Banathy, Intersystem Publ.: Seaside,
CA, 2, 573 (1985).
43. R. Hefferlin, Periodic Systems and Their Relation to the Systematic
Analysis of Molecular Data, Edwin Mellin Press: Lewiston, New York, 1989.
44. (a) S. A. Shchukaryov, J. Russ. Phys. Chem. Soc., 55, 447
(1924); (b) K. Guggenheimer, J. Phys. et Radium, 5, 253 (1934);
(c) W. M. Elsasser, ibid. 5, 389 (1934); ibid. 5,
635 (1934); (d) I. P. Selinov, Russ. J. Exp. Theor. Phys. 4, 666
(1934); (e) M. L. Chepelevetckii, Russ. J. Phys. Chem., 40 (2),
307 (1966).
45. I. P. Selinov, Periodic System of Isotopes, Acad. Sci. USSR Publ.:
Moscow, 1962 (in Russian).
46. V. K. Grigorovich, Periodic Law of Mendeleev and Electronic Structure
of Metals, Nauka Publ.: Moscow, 1966 (in Russian).
47. Ch. Gerhardt, Precis de Chimie organique (in French), Paris, 1844.
48. A. M. Butlerov, Selected Works, Academy of Science Publ.: Moscow,
1958, Vol. 3, p. 241 (in Russian).
49. (a) J. B. A. Dumas, Ann., 105, 74 (1858); (b) M. Pettenkofer,
ibid.
p. 187; (c) J. A. R. Newlands, J. Chem. Soc (London) 15, 36 (1862);
(d) G. Pelopidas, J. Russ. Chem. Soc., 15 (1), 364 (1883).
50. E. V. Babaev, in History and Methodology of Natural Sciences, Vol.
35, Philosophical Problems of Chemistry, Ed. A. P. Rudenko, Moscow University
Press: Moscow, 1988, pp. 121-140 (in Russian).
51. E. V. Babaev, in Principles of Symmetry and Systemology in Chemistry,
Ed. N. F. Stepanov, Moscow University Press: Moscow, 1987, pp. 203-227
(in Russian). [Chem. Abstr. 109: 27902b]
52. R. Hefferlin, E. V. Babaev, and G. V. Burdick, Periodic Systems
of Molecules: Physical and Chemical, Reports of Phys. Dept. Southern College,
No. 1, Collegedale, TN, 1994, 37 pp.
53. A. Gorsky, Modern Systems of Classification of Chemical Compounds,
Naukowe: Warsaw, 1971 (in Polish).
54. N. A. Morozov, Periodic Systems of Structure of Matter, Sytin Publisher:
Moscow, 1907 (in Russian).
55. (a) N. A. Morozov, Letters from Captivity, Sytin Publishers: St.
Petersburg, 1907 (in Russian); (b) S. I. Wolfkovitch, Reports on Scientific
Works of Members of the Mendeleev Chemical Society, 4, 22, (1949)
(in Russian); (c) L. P. Petrov, in Doctrine of Periodicity: History and
Modernity, Nauka: Moscow , 1981, p. 37 (in Russian); (d) V. A. Volkov,
E. V. Vonskii, G. I. Kuznetsova, Outstanding Chemists of the World, Vysshaya
Shkola Publ.: Moscow, 1991 (in Russian).
56. H. Decker, Helv. Chim. Acta, 5, 201, 285 (1922).
57. (a) A. Haas, Chem. Zeit. 106, 239 (1982); (b) A. Haas, Adv.
Inorg. Chem. Radiochem., 28, 167 (1984); (c) A. Haas, Pure Appl.
Chem. 63, 1577 (1991).
58. (a) F. M. Shemyakin, Russ. J. Gen. Chem. 1, 3459 (1931);
ibid.2,
128 (1931), ibid. 3, 269 (1933), ibid.4, 1034
(1934); (b) F. M. Shemjakin, Z. fur Phys. Chem. 152, 235 (1931);
(c) H. G. Grimm, ibid. 154, 478 (1931).
59. A. Gorsky, Annal. Soc. Chim. Polon. 45, 1981 (1971); ibid.46,
127 (1972).
60. W. Haberditzl, Structure of Matter and Chemical Bonding (in German),
VEB Verlag: Berlin, 1972.
61. M. J. S. Dewar, Molecular Orbital Theory of Organic Chemistry, McGraw
Hill: New York, 1969.
62. (a) K. Wade, Adv. Inorg. Chem. Radiochem., 18, 1 (1976);
R. E. Williams, ibid. p.67; R. W. Rudolf, Acc. Chem. Res., 12,
446 (1976).
63. (a) D. Rouvray, Computational Chemical Graph Theory, Nova Sci. Publ.:
Commack, NY, 1990; (b) N. Trinajctic, Chemical Graph Theory, 2nd Ed., CRC
Press: Boca Raton, FL, 1991; (c) Chemical Graph Theory: Introduction and
Fundamentals, Eds. D. Bonchev, D. Rouvray, Abacus Press/Gordon and Beach:
New York, 1991.
64. (a) Y. C. Martin, Quantitative Drug Design: A Critical Introduction,
Dekker: New York, 1978; (b) R. Franke, Theoretical Drug Design Methods,
Elsevier: Amsterdam, 1984.
65. Concepts and Applications of Molecular Similarity, Eds. M. A. Johnson
and G. M. Maggiora, Wiley Interscience, J. Wiley and Sons: New York, 1990.
66. H. A. Bent, J. Chem. Educ. 43 (4), 170 (1966).
67. I. Langmuir, J. Amer. Chem. Soc., 41, 868, 1543 (1919).
68. (a) F. Kober, Prax. Naturwiss. Chem., 7, 199 (1981); (b)
H. Shmidbaur, Fortchr. Chem. Forsh. 13 (1), 167 (1969); (c) R. G.
Gillis, J. Chem. Educ. 37 (3), 66 (1958); (d) H. L. Bradlow, C.
A. Vanderwerf, and J. Kleinberg, ibid. 24 (9), 433 (1947).
69. (a) H. G. Grimm, Z. Electrochem., 31, 474 (1925); (b) H.
G. Grimm, Naturwiss. 17, 557 (1929).
70. R. J. Buenker, S. D. Peyerimhoff, Theor. Chim. Acta 24, 132
(1972); idem. J. Chem. Phys., 48 (1), 354 (1968).
71. Nicolaus von Kues, De Docta Ignorantia, I, 7, 18-19. Philosophisch-Teologische
Schriften, Wien, 1964-1967 (in Latin).
72. G. Endrus, Partition Theory, Nauka: Moscow, 1982 (in Russian).
73. F. Klein, Elementary Mathematics from Higher Viewpoint. Vol. 1,
3-te Aufl., Springer Verlag: Berlin, 1924 (in German).
74. F. Harary, Graph Theory, Addison-Wesley: Reading, MA, 1969.
75. P. J. Giblin, Graphs, Surfaces and Homology: An Introduction to
Algebraic Topology, Chapman and Hall: London, 1981.
76. E. V. Babaev, in Graph Theoretical Approaches to Chemical Reactivity,
Vol. 9, Understanding Chemical Reactivity, Eds. D. Bonchev and O. Mekenyan,
Kluwer Academic: Dordrecht-Boston-London, 1994, pp. 209-220.
77. Yu. A. Zhdanov, Homology in Organic Chemistry, Moscow University
Press: Moscow, 1950 (in Russian).
78. (a) Boron Hydrides Chemistry, Ed. E. L. Mutterties, Academic Press:
New York, 1975; (b) W. N. Lipscomb, Boron Hydrides, Benjamin: New York,
1963.
79. G. A. Olah, G. K. S. Prakash, R. E. Williams, L. D. Field, and K.
Wade, Hypercarbon Chemistry, J. Wiley and Sons: New York, 1987.
80. (a) R. E. Rundle, Record Chem. Prog. 23 (4), 195 (1962);
(b) C. K. Jorgensen, Chimia, 25 (4), 109 (1971); (c) D. A. Bochvar,
N. P. Gambaryan, L. M. Epstein, Russ. Chem. Rev., 45 (7), 1316 (1976).
81. (a) R. S. Mulliken, Rev. Mod. Phys., 14, 204 (1942); (b)
A. D. Walsh, J. Chem. Soc., 2260 (1953); A. D. Walsh, Prog. in Stereochem.,
1,
1 (1954); (c) G. Herzberg, Molecular Spectra and Molecular Structure. Part
III., D. van Nostrand: Princeton, New Jersy, 1965; (d) B. M. Gimarc, J.
Amer. Chem. Soc., 92, 266 (1970); (e) R. G. Pearson, Symmetry Rules
for Chemical Reactions, J. Wiley and Sons: New York, 1976.
82. (a) R. J. Gillespie, R. S. Nyholm, Quart. Rev. Chem. Soc., 11,
339 (1957); (b) R. J. Gillespie, Molecular Geometry, van Nostrand - Reinhold:
Princeton, New Jersy, 1972; (c) R. J. Gillespie, I. Hargittai, The VSEPR
Model of Molecular Geometry, Allyn and Bacon: Boston - London, 1991.
83. R. F. W. Bader, R. J. Gillespie, and P. G. Macdougal, in From Atoms
to Polymers: Isoelectronic Analogies, Vol. 11, Molecular Structure and
Energetics, Eds. J. F. Liebman, A. Greenberg, VCH Publishing: New York,
1989, pp. 1-51.
84. (a) Chemical Applications of Topology and Graph Theory, Vol. 28,
Studies in Physical and Theoretical Chemistry, Ed. R. B. King, Elsevier:
Amsterdam, 1983; (b) D. M. P. Mingos and R. L. Johnson, Theoretical Model
of Cluster Bonding, Structure and Bonding, Springer-Verlag: Berlin, 1987,
p. 29.
85. E. V. Babaev, Chemical Concepts from the Viewpoint of Surfaces'
Topology, 6th International Conference on Mathematical Chemistry, Pitlocry,
Scotland, July 10-14, 1995, plenary lecture (in preparation for J. Chem.
Inf. Comput. Sci.).
86. (a) Ya. K. Syrkin, in 100 Years of the Periodic Law of Chemical
Elements, Proceed. X-th Mendeleev Congress, Ed. N. N. Semenov, Nauka Publ.:
Moscow, 1969, p. 85 (in Russian); (b) D. N. Shigorin, Russ. J. Phys. Chem.,
51,
1115 (1977); ibid. 54, 1087, 1095 (1980); (c) V. M. Kaslin, Preprints
302, 303, Optical Laboratory, Physical Institute: Moscow 1983 (in Russian);
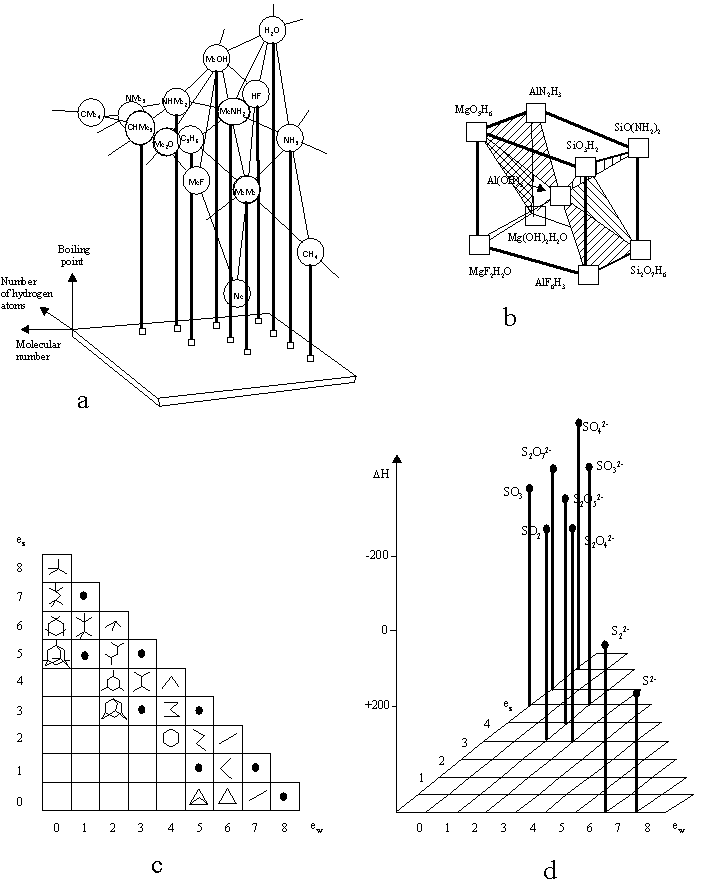
(d) Figure 4 and Ref. 3 in R. Hefferlin, J. Chem. Inf. Comput. Sci, 34,
314 (1994); (e) C. H. D. Clark, Trans. Faraday Soc., 4, 1017 (1935).
87. (a) S. A. Shchukaryov, Inorganic Chemistry, Vols. 1, 2, Vysshaya
Shkola: Moscow, 1970 (in Russian); (b) R. T. Sanderson, Inorganic Chemistry,
Reinhold: New York, 1967.
88. A. Boldyrev, N. G. Gonzales, and J. Simons, J. Phys. Chem. 98,
9931 (1994).
89. (a) R. Hefferlin, J. Quant. Spectrosc. Radiat. Transfer 16,
1101 (1976); (b) R. Hefferlin et. al. ibid. 21, 315 (1979);
(c) ibid. 21, 337 (1979); (d) R. Hefferlin, H. Kuhlman, ibid.24,
379 (1980); (e) R. Hefferlin, W. Innis, ibid. 24, 97 (1983);
(f) R. Hefferlin, M. Kutzner, J. Chem. Phys. 75, 1035 (1981).
90. (a) M. W. Chase et. al., J. Phys. Chem. Ref. Data 7, 793
(1978); (b) M. W. Chase et. al., J. Phys. Chem. Ref. Data 14, Supplement
No. 1 (1985).
91. F. A. Kong, J. Mol. Struct. 90, 17 (1982).
92. (a) R. Hefferlin, et. al., J. Quant. Spectrosc. Radiat. Transfer,
32,
257 (1984); (b) R. Hefferlin, in McGraw-Hill Yearbook of Science and Technology,
McGraw-Hill: New York, NY 1989, p.224.
93. (a) G. V. Zhuvikin, R. Hefferlin, Bull. Leningrad University, 16,
10 (1983) (in Russian); (b) R. Hefferlin, in Proc. XVIIth International
Colloquium on Group Theoretical Methods in Physics (June 27 to July 2,
1988, Sainte-Adele, Canada), Eds. Y. Saint-Aubin, L. Vinet, World Scientific:
Singapore, 1989, p. 652. (c) G. V. Zhuvikin, R. Hefferlin, in Proc. XIXth
Intern. Coll. Group Theor. Methods in Physics (Salamanca, Spain, 1992),
Eds. M. A. del Olmo, M. Santander, and J. M. Guilarte, vol. II. Anales
de Fisica, Monographias 1, Real Sociedad Espanola de Fisica: Madrid, 1992,
p. 358; (d) C. M. Carlson, R. J. Cavanaugh, R. A. Hefferlin, and G. V.
Zhuvikin, in XXth Intern. Coll. Group Theoretical Methods in Physics (Yamada
conference XL, 1995), Eds. A. Arima, T. Eguchi, and N. Nakanishi, World
Scientific: Singapore, 1995, p. 211.
94. C. M. Carlson, R. J. Cavanaugh, and R. A. Hefferlin, Periodic systems
of molecular states from the boson group dynamics of SO(3) SU(2)s, J. Chem.
Inf. Comp. Sci., (accepted for publication 12 September 1995).
95. (a) G. V. Zhuvikin and R. Hefferlin, Symmetry principles for periodic
systems of molecules, Joint Report #1 of the Physics Departments of Southern
College, Collegedale, TN, USA and St. Petersburg University, St. Petersburg,
Russia, Sept. 11, 1994 (widely distributed to university and institute
libraries); (b) C. M. Carlson, R. Hefferlin, and G. V. Zhuvikin, Analysis
of group theoretical periodic systems of molecules using tabulated data,
Joint Report #2 of the Physics Departments of Southern College, Collegedale,
TN, USA and St. Petersburg University, St. Petersburg, Russia, March, 1995
(widely distributed to university and institute libraries).
96. R. A. Hefferlin, A.V. Sepman, and G.V. Zhuvikin, Molecular multiplets
of Alkaline atoms, J. Chem. Inf. Comp. Sci. (accepted for publication 30
September 1995).
97. E. V. Babaev, Mendeleev Chemistry Journal, 38 (6), 785 (1994),
(English translation).
98. E. V. Babaev, D. E. Lushnikov, N. S. Zefirov, J. Amer. Chem. Soc.,
115
(6), 2416 (1993).