Eugene Babaev "Intuitive Chemical Topology Concepts" (c)7. Invariance of the Euler Characteristics in Chemical Reactions
A chemist clearly distinguishes a chain from an ordinary cycle in respect to their interconversion in the chemical reaction. Thus, a cyclization is opposite to a ring cleavage reaction, and a recyclization (changing a cycle to another cycle) is intuitively different from a formation or destruction of a cycle. Similarly, a reaction with the change in the number of components (like an addition or elemination) is clearly different from a process with the preservation of the number of components (like a substitution or isomerization). Therefore, in the common sense, the cyclicty and connectedness are variable parameters in chemistry, that may freely appear or disappear upon a reaction. The precursors of the same molecule may be topologically different, cyclic or not, connected or disconnected. No restrictions are evident to the interconversion of components and cycles: a cycle may be formed from a connected molecule (another cycle, chain, or even polycycle) or from several disjoint molecules (chains and/or cycles).
By contrast, in the model of molecular topoids, every change in the cyclicity and connectedness is strictly predetermined by equations (11). Consider a chemical equation of any reaction as the interconversion of one set of molecular topoids to another one. Assume that the bonds in the initial and final ensembles are the localized (2c,2e) bonds, the sets may be disconnected, and some electrons may be unpaired. Let Z and N be the total number of valence electrons and atoms in the initial ensemble. A reaction is a rearrangement of electrons between atoms within the initial ensemble, leading to the final ensemble. According to the common material balance equation of a reaction, the values Z and N should remain the same in the final ensemble. Any ensemble follows equation (11) c = 2N -- Z. If there are no changes in Z and N upon a reaction (DZ = DN = 0), then, there are also no changes in the Euler characteristic and Dc = 0. In other words, within the model of molecular topoids, the Euler characteristic should be invariant in a chemical reaction.
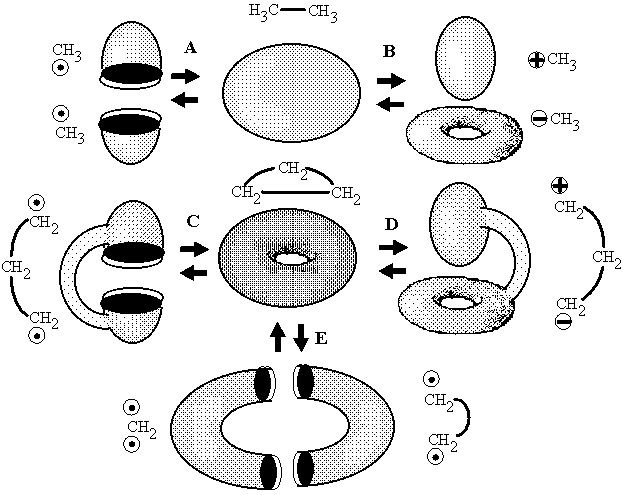
Figure 19. Examples of five possible types of interconversion of handles, holes, and components in molecular topoids with preservation of the Euler characteristic as illustrations of equations (12a)--(12e).
The structural changes via reactions from the topological viewpoint are the interchanges of C handles (ordinary cycles, multiple bonds, lone pairs), L unpaired electrons, and K components. The equation (11) implies that c = 2K -- 2C -- L. Therefore, any rearrangement of electrons and bonds should follow the same topological balance equation (12):
(12) Dc = 2DK -- 2DC -- DL = 0
Clearly, the components, handles (lone pairs, double bonds, and cycles) and unpaired electrons can not spontaneously appear or disappear without leaving a trace (in contrast to conventional models). Any change in C, L, K is strictly predetermined by the conservation law (12). Let us consider some examples (Figure 19).
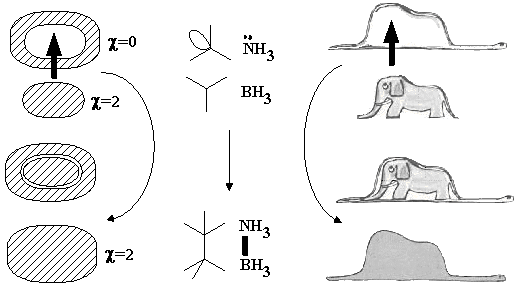
Loss of connectedness (case of boa and elephant). By definition, a localized bond is the (2c,2e) bond. In the classical Lewis concept, a bond can be formed either by recombining two radicals, or by donating an electron pair from a Lewis base to an acid. Within the model of molecular topoids, the homolytic formation (from radicals) resembles gluing of a globe from two hemispheres that are pasted to each other by 1D boundaries around the holes (Figure 19 A). Heterolytic bond formation (BH3 + NH3 = BH3NH3 or a methyl cation and anion forming ethane) is equivalent to the combination "sphere + torus = new sphere" (Figure 19 B). The visual image of the process may resemble nut-and-bolt manipulations (with the disappearance of a hole in a nut), however the difference is that cylindrical walls around the area of contact are supposed to "dissolve" inside the newly formed sphere. An interesting and more pronounced visualization may be found in The Little Prince by Antoine de Saint-Exupéry: "a boa constrictor digesting an elephant" looks like a hat (Figure 20).
Figure 20. The surface of sphere pasted to the hole of a toroidal surface results in a new spherical surface with preservation of the Euler characteristic. The process is shown for different cases, which are topologically indistinguishable.
In both cases, of homolytic or polar formation of a bond (Figures 19 A, B), the value Dc = 0, because for topoids of reagents and a product c({1S,1S}) = c ({S0,S1}) = c (S0) = 2. In both cases the initial number of components decreases (DK = 1). However, this decrease is compensated by immediate disappearance of holes. These are either two holes of the hemispheres (and the balance equation is reduced to 2DK = DL = 2) or one hole -- a handle -- of a torus (then the equation is DK = DC = 1). Hence, the equation (12) is valid for both cases. Therefore, in chemistry the connectedness cannot appear from a disconnectedness in a simple way (like A + B = C): the price to be paid is the destruction of holes. Of course, the same balance equation describes the reverse processes of homolytic or heterolytic bond cleavage.
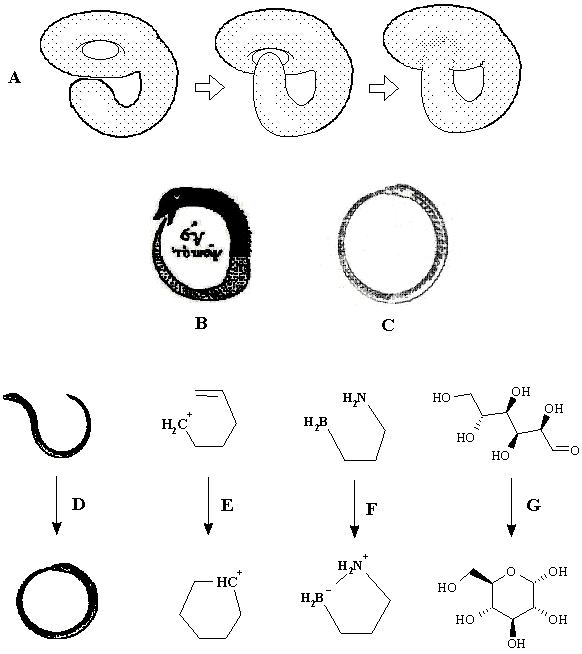
Formation of cycle (Uroboros paradox). The appearance of cycles may be simply reduced to the previous cases by connecting two free radical centers (or two dual polar centers) by a chain. An analogy with taking a connected sum of surfaces is evident. The connected sum of two hemispheres (1S # 1S ~ 2S) is a cylinder (Figure 19 C). The connected sum of sphere and torus (S1 # S0 ~ S1) is again a torus (although it may be distorted as shown in Figure 19 D). Now, paste the ends of a chain as described above and obtain a cycle (torus) in both cases. Evidently, Dc = 0. In the first case the balance equation is 2DC = -- DL, and the appearance of one toroidal hole (birth of molecular cyclicity) is compensated by destruction of two other holes of a cylinder. The second case corresponds to the balance equation DC = 0 (because there are no changes in K or L) and is curious. Trying to destroy the initial hole (by locating a stretched fragment of a torus in its own cavity) we create a new hole! (Figure 21 A). By other words, a hole is preserved upon gluing, and hence, a cycle cannot be created or destructed in the intramolecular hetorolytic reactions (where DK = DL = 0), it may only change the size.
The last statement seems contradicting to the chemical intuition: what about common cyclizations, where a cycle is formed from a chain? Let us call this case the Uroborus paradox. The Uroborus -- a serpent devouring its tail (Figure 21 B, C) is an archetypal alchemical symbol, famous in the story of Kekule’s dream. At first glance, the process on Figure 21 D serves as an image of forming a cycle from an acyclic structure (cf. the ring closure processes in Figure 21 E, F, G). However, if one consider all cycles in the molecular pseudographs (handles in topoids), this analogy is false: reactions 20 E -- G are examples of cycle preservation (although the size of a cycle is changed). Furthermore, the intuitive analogy to Uroborus fails by another reason. From the standpoint of topology, any serpent has a tunnel inside it, and the total 2D surface of its 3D body is homeomorphic to a torus. (By the same reason the boa in Figure 20 is not homeomorphic to a hat.) This fact, evident in biology long ago [113], is important in the modern topological classifications of biological species [114]. Therefore, all cases D -- G in Figure 21 (either chemical or biological) are better represented as gluing to itself of a deformed and stretched torus (Figure 21 A).
Figure 21. (A) The preservation of a hole via an attempt of pasting a fragment of the same surface into the toroidal cavity and the "Uroboros paradox" (see text). The image of Uroborus in pre-Christian alchemical tradition (B) and in Medieval-Christian mysticism (C). The paradox is manifested in the preservation of a handle (in the topoid) or the cyclomatic number (in the molecular pseudograph) in apparent "cyclizations": (D) an inessential deformation of the initially toroidal 2D surface of a biological object, (E) the intramolecular electrophilic addition to a double bond (cycle c2 is changed to c6), (F) the intramolecular interaction of a Lewis base and acid (cycle c1 is changed to c5), (G) the cycle-chain tautomerism of glucose (the same conversion of cycles as in the case E).
Topological balance equations. The existence of the same "topological balance" for reversed processes (homolytic or heterolytic cleavage of a cycle) is evident. We may prove [31] that the four examples above and the last one in Figure 19 E completely exhaust all types of interconversion of invariants K, C, L. Indeed, if one of values (K, C, or L) is not changed, we may equalize it to zero in equation (12) and consider the remaining pair of invariants to be interconverted:
(12a) 2DK = DL (Figure 19 A)
(12a) DC = DK (Figure 19 B)
(12b) 2DC = -- DL (Figure 19 C)
We may also consider that nothing is changed (just the above example of the serpent),
(12d) 2DC = 2DK = DL = 0, (Figure 19 D)
and finally, that everything may be interchanged, so that
(12e) 2DK -- 2DC -- DL = 0. (Figure 19 E)
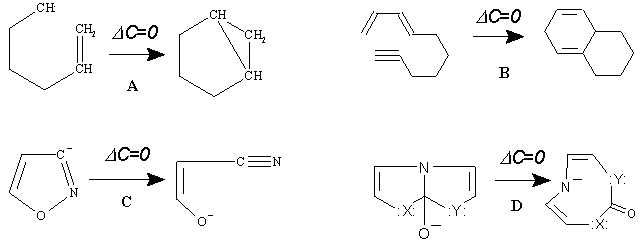
No other possibility is permitted, and spontaneous "birth or death" of only one invariant is prohibited. Lest there be any doubt, a few examples of balance for some specific cases are presented in Figure 22. These structural equations, which look like ring closure and ring opening reactions, in fact are ring preservations from topological viewpoint and should be referred to as recyclizations (expanding the author’s early classification of heterocyclic ring transformations [115]).
Figure 22. Some reactions related to the "Uroborus paradox" treated as a conservation of the handles (in topoids) or of the cyclomatic number (in molecular pseudographs) in the intramolecular reactions (DK = 0). In none of the reactions ("bicyclizations" A, B or "ring-opening" reactions C, D) is the number of cycles changed (DC = 0).